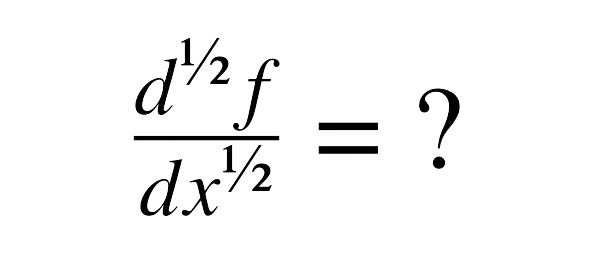
Wavelets Theory

Posted on by math
Wavelets Theory

Wavelets Theory , is a relatively new and emerging area in mathematical research. As a powerful tool, wavelets have been extensively used in signal processing, numerical analysis and many other areas. Wavelets theory is a relatively new and an emerging area in mathematical research. Wavelets allow the accurate representation of a variety of functions and operators.

5.1 Introduction

Wavelets establish a connection with fast numerical algorithms. Hafshejani et al. [1] applied the Legendre wavelet methods to obtain the numerical solution of Delay differential equations. Soleymanivaraki et al. [2] implement the Lengendre wavelets method to solve fractional order differential equations. Razzaghi and Yousefi used Legendre wavelets method [3-4]. In addition, Chebyshev, Legender and Shannon wavelet method have been used for obtaining the numerical solutions of the Fredholm integral equation in [5]. Kajani and Mahdavi [6] solved the nonlinear integral equations by using Galerkin method with hybrid Block-Pulse function.  Mohammadi et al. [7] used Legendre wavelet Galerkin method for solving the ordinary differential equations. Hosseini et al. [15] solved the telegraph equations with a new Rothe-wavelet method. Venkatesh et al. [8] used Legendre Wavelets Based Approximation Method for Cauchy Problems.

In this chapter, I modified original Legendre wavelet method by inserting Monic polynomials which gives us very reliable solutions. Monic Wavelet Method (MWM), is used for solving singular ordinary differential equations, higher order BVPs, integral equations, Delay differential equations (DD), second-order differential equations with Robin conditions, nonlinear integral equations. It is to be observe that the proposed technique has been applied on a wide range of nonlinear diversified physical problems including, high-dimensional nonlinear evolution equation. It is to be highlighted that suggested algorithm is extremely simple but highly effective and may be extended to other singular problems of diversified physical nature. Moreover, this new scheme is capable of reducing the computational work to a tangible level while still maintaining a very high level of accuracy.

5.2 Monic Wavelet Method

We proposed a new algorithm by inserting Monic polynomials in traditional Legendre wavelets method. This technique is successively applied to find the exact solution singular ordinary differential equations. The proposed technique is very simple and highly compatible for solving such kind of problems.

5.2.1 Methodology

Definition 5.1. Recurrence formula of Monic polynomial is defined as

M_n(x)=(1-z)(x+1)^n+z(x-1)^n    (5.1)

few Monic polynomials given below

M_0=1,

M_1=x-1,

M_2=x^2-2x+1,

M_3=x^3-3x^2+3x-1,

M_4=x^4-4x^3+6x^2-4x+1,

.

.

..

Definition 5.2. In recent years, wavelets have found their way into many different fields of science and engineering [9-10]. Wavelets constitute a family of functions constructed from the dilation and translation of a single function called the mother wavelet. When the dilation parameter a and the translation parameter b vary continuously, we have the following family of continuous wavelets:

\psi _{a,b}(t)=|a|^{-\frac{1}{2}}\psi ((t-b)/a) a,b∈R,\ a\ne 0.      (5.2)

Monic wavelets ψ_{nm}(t)=ψ(k,n,m,t)  have four arguments; n,k can assume any positive integer, m is the order for Monic polynomials and t is the normalized time. They are defined on the interval [0, 1) by;

\psi _{nm}(t)=\sqrt{(}m+1/2)2^{\frac{k}{2}}M_m(2^kt-(2n+1))\ \ \ \ n/2^k\le t\le (n+1)/2^k  (5.3)

where m=0,1,2,\dots ,M and n=0,1,\dots ,2^k-1. The coefficient (m+\frac{1}{2})  is for orthonormality. Here M_m(t) are the well-known Monic polynomials of order m, which have been previously described.

Definition 5.3. A function  define over [0,1) may be expanded as

f(t)=\sum _{n=1}^∞\sum _{m=0}^∞c_nm\psi _nm(t),      (5.4)

where c_{nm}=〈f(t),\psi _{nm}(t)〉,  in which 〈∙,∙〉 denotes the inner product. If the infinite series in Eq. (5.4) is truncated, then Eq. (5.4) can be written as

f(t)=\sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M-1}c_{nm}\psi _{nm}(t).    (5.5)

It can be written as

f(t)=\sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M-1}c_{nm}\psi _{nm}(t)=C^T\psi (t).    (5.6)

where C and ψ(t) are 2^{k-1}M\times 1 matrices given as

5.3 Applications

Example 5.1 Consider the following singular initial value problem  [11] as

y^{^{\prime }\prime }(x)+\frac{4}{x}y^{^{\prime }}(x)+\frac{2}{x^2}y(x)=12,    (5.9a)

subject to the boundary conditions

y(0)=1,\ y^{^{\prime }}(0)=0.      (5.9b)

The exact solution of Eq. (5.9a) is

y(x)=x^2.      (5.10)

According to the Monic Wavelets Method , we assume the trial solution

y(x)=\sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M-1}c_{nm}\psi _{nm}(x)=C^T\Psi (x).    (5.11)

where C and ψ(t) are 2^{k-1}M\times 1 matrices given as

C=\left[c_{10},c_{11},\dots ,c_{1M-1},c_{20},c_{21},\dots ,c_{2M-1},\dots ,c_{2^{k-1}0},\dots ,c_{2^{k-1}M-1}\right]^T ,

and

\psi \left(x\right)=\left[\psi _{10},\psi _{11},\dots ,\psi _{1M-1},\psi _{20},\psi _{21},\dots ,\psi _{2M-1},\dots ,\psi _{2^{k-1}0},\dots ,\psi _{2^{k-1}M-1}\right]^T.

We apply the proposed technique to solve Eq. (5.9) with K=1 and M=10,we have Eq. (5.11) is

y(x)=\sum _{n=1}^1\sum _{m=0}^9c_{nm}\psi _{nm}(x),=c_{10}\psi _{10}(x)+c_{11}\psi _{11}(x)+c_{12}\psi _{12}(x)+⋯=C^T\Psi (x),    (5.12)

where

\psi _nm(x)=\sqrt{(}m+\frac{1}{2})2^{\frac{k}{2}}A_m(2^kt-(2n+1)).    (5.13)

From Eq. (5.12) we obtained

y(x)=c_{10}-2\sqrt{3}c_{11}+2\sqrt{3}xc_{11}+4\sqrt{5}c_{1,2}-8\sqrt{5}c_{12}x+4\sqrt{5}x^2c_{12}+⋯=C^T\Psi (x),

where

C=[c_{10},c_{11},c_{12},⋯]^Tand\ \ \ \Psi (x)=[1,-2\sqrt{3}+2\sqrt{3}x,4\sqrt{5}-8\sqrt{5}x+4\sqrt{5}x^2,⋯]^T.

Substituting into the given problem we get

C^T\Psi ^{^{\prime }\prime }(x)+\frac{4}{x}C^T\Psi ^{^{\prime }}(x)+\frac{2}{x^2}C^T\Psi (x)=12,    (5.14a)

subject to the boundary conditions

C^T\Psi (0)=1,C^T\Psi ^{^{\prime }}(0)=0.    (5.14b)

Substitute the collocating points are in Eq. (5.14a), we have the system of equations

x_i=\cos ⁡(\frac{\left(2i+1)\pi \right)}{2^kM}),i=3.    (5.15)

A_{3\times 3}C_{3\times 1}=b_{3\times 1}.

After solving we get the following exact solution.

y(x)=x^2.

Example 5.2 Consider the following singular initial value problem[11] as

y^{^{\prime }\prime }(x)+\frac{2}{x}y^{^{\prime }}(x)+y(x)=6+12x+x^2+x^3,    (5.16a)

subject to the boundary conditions

y(0)=1,y^{^{\prime }}(0)=0.    (5.16b)

The exact solution of Eq. (5.16a) is

y(x)=x^2+x^3.    (5.17)

According to the Monic Wavelets Method (MWM), we assume the trial solution

(x)=\sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M-1}c_{nm}\psi _{nm}(x)=C^T\psi (x).    (5.18)

where C and ψ(t) are 2^{k-1}M\times 1 matrices given as

C=\left[c_{10},c_{11},\dots ,c_{1M-1},c_{20},c_{21},\dots ,c_{2M-1},\dots ,c_{2^{k-1}0},\dots ,c_{2^{k-1}M-1}\right]^T ,

and

\psi \left(x\right)=\left[\psi _{10},\psi _{11},\dots ,\psi _{1M-1},\psi _{20},\psi _{21},\dots ,\psi _{2M-1},\dots ,\psi _{2^{k-1}0},\dots ,\psi _{2^{k-1}M-1}\right]^T.

We apply the proposed technique to solve Eq. (5.9) with K=1 and M=10,we have Eq. (5.18) is

y(x)=\sum _{n=1}^1\sum _{m=0}^9c_{nm}\psi _{nm}(x),=c_{10}\psi _{10}(x)+c_{11}\psi _{11}(x)+c_{12}\psi _{12}(x)+⋯=C^T\Psi (x),    (5.19)

where

\psi _nm(x)=\sqrt{(}m+\frac{1}{2})2^{\frac{k}{2}}A_m(2^kt-(2n+1)).    (5.20)

From Eq. (5.19) we obtained

y(x)=c_{10}-2\sqrt{3}c_{11}+2\sqrt{3}xc_{11}+4\sqrt{5}c_{12}-8\sqrt{5}c_{12}x+4\sqrt{5}x^2c_{12}+⋯=C^T\Psi (x),

where

C=[c_{10},c_{11},c_{12},c_{13},⋯]^T    and   \Psi (x)=[1,-2\sqrt{3}+2\sqrt{3}x,4\sqrt{5}-8\sqrt{5}x+4\sqrt{5}x^2,⋯]^T.

Substituting into the given problem we get

C^T\Psi ^{^{\prime }\prime }(x)+\frac{2}{x}C^T\Psi ^{^{\prime }}(x)+C^T\Psi (x)=6+12x+x^2+x^3,    (5.21a)

subject to the boundary conditions

C^T\Psi (0)=1,C^T\Psi ^{^{\prime }}(0)=0.    (5.21b)

Substitute the collocating points are in Eq. (5.21a), we have the system of equations

x_i=\cos ⁡(\frac{(2i+1)\pi }{2^kM}),i=2,3.    (5.22)

Implementing the collocating points and imposing the initial value of the system, the matrix form is given as

A_{4\times 4}C_{4\times 1}=b_{4\times 1}.

After solving we get the following exact solution

y(x)=x^2+x^3.

References

[1]. M.S. Hafshejani, S. K. Vanani and J. S. Hafshejani, Numerical Solution of Delay Differential Equations Using Legendre Wavelet Method, World Applied Sciences Journal 13 (Special Issue of Applied Math): (2011), 27-33.

[2]. M.Soleymanivaraki, H. Jafari, M. A. Firoozjaee, Legendre wavelets for solving fractional differential equations, Journal of Applied Mathematics, Islamic Azad University of Lahijan, 7(4)(27)(2011).

[3]. M.Razzaghi and S. Yousefi, Legendre wavelets direct method for variational problems, mathematics and computers in simulation, 53(2000), 185-192.

[4]. M. Razzaghi and S. Yousefi, Legendre wavelets method for the solution of nonlinear problems in the calculus of variations, Math. Comput. Model. 34(2001), 45-54.

[5]. K.Paryab, M. Rostami, Expansion method for linear fredholm integral equations of second kind by Chebyshev, Legendre and Shannon wavelets and the comparison of their numerical results, Mathematical Sciences 2 (4) (2008), 335-346.

[6]. M.Tavassoli Kajania, S. Mahdavi, Numerical solution of nonlinear integral equations by Galerkin methods with hybrid Legendre and block-pulse functions, Mathematics Scientic Journal Vol. 7 (1) (2011), 97-105.

[7]. F. Mohammadi, M. M. Hosseini and S. T. Mohyud-din, Legendre wavelet galerkin method for solving ordinary differential equations with non analytic solution, Int. J. Syst. Sci. 42 (4)( 2011), 579-585.

[8]. G. Venkatesh, S. K. Ayyaswamy, S. Raja Balachandar and K. Kannan, Legendre wavelets based approximation method for Cauchy problems, applied mathematical sciences, 6(126)(2013), 6281 – 6286.

[9]. F.Mohammadi and M. M. Hosseini, A new Legendre wavelet operational matrix of derivative and its applications in solving the singular ordinary differential equations, J. Franklin Inst. 348(2011), 1787-1796.

[10]. F.Mohammadi, M. M. Hosseini. A comparative study of numerical methods for solving quadratic Riccati differential equations. J. Franklin Inst., 348(2011), 156-164.

[11]. Yahya Qaid Hasan and Liu Ming Zhu, Modified Adomian’s decomposition method for singular initial value problems in the second-order ordinary differential equations, Surveys in Mathematics and its Applications, 3(2008), 183- 193.

Leave a Reply

Your email address will not be published. Required fields are marked *