The Convolution Theorem Formula

Posted on by math

The Convolution Theorem Formula, the Convolution Theorem is an important part of mathematics which connects theory with practice in regards to signal processing or data analysis. Although convoluted in wording, it is definitely one of the most crucial theorems that help opt for easier methods while doing complex calculations for convolution operations and transformations at shard level in different scientific and engineering problems.

In case you are eager to learn more about the basics, practical uses, and importance of the Convolution theorem, this hand out attempts to explain the theorem in the most straight forward manner possible. By reading it, you will have knowledge of what the convolution theorem formula is and how it is used.

What is the Convolution Theorem?

The convolution theorem describes that the result of convolution in the time domain corresponds to multiplication in the frequency domain or vice versa in the case of Fourier or Laplace transform operations. This principle is beneficial for mathematics as it reduces tough calculations especially in fields such as signal processing and communications.

Put simply, we can operate in both time and frequency domains and determine which ever domain assists us simplify calculations.

The Convolution Formula

Before getting into the convolution theorem, it is best to start with the convolution operation and how it is mathematically expressed:

1. Convolution in the Time Domain

The convolution of two functions \( f(t) \) and \( g(t) \) is defined as:

(f * g)(t) = \int_{-\infty}^\infty f(\tau)g(t - \tau)d\tau
This equation calculates a partial weighted overlap or summation of one signal with respect to some other signal which has been displaced. Let’s break it down:

( f(\tau) \) and \( g(t - \tau) \) are the astrophysical functions.

\( \tau \) is the variable that acts as a potential target for integration.

The output ( (f * g)(t) \) is another function after going through an operation.

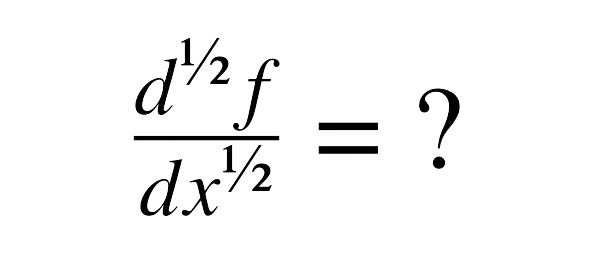
2. The Convolution Theorem Formula

At this point, things get interesting. The convolution theorem tells us that:

\mathcal{F}\{f * g\} = \mathcal{F}\{f\} \cdot \mathcal{F}\{g\}

And alternatively:

\mathcal{F}^{-1}\{F(\omega) \cdot G(\omega)\} = f(t) * g(t)

In this context, \( \mathcal{F} \) is the symbol for the Fourier transform.

Transformations F and G are the Fourier transforms of functions f and g respectively.

In short, convolution in time domain is multiplication in a frequency domain, and convolution in a frequency domain is multiplication in a time domain.

This is quite useful in most practical scenarios because computation of a convolution integral, which is quite intensive, can simply be transformed into multiplication.

Why Does the Convolution Theorem Matter?

Now, what comes next is why does it matter and why is it so important? Why is it integral to be familiar with these theorem? The simplifications is the answer at first. Along now in separating two different areas, they call it a bridge. In engineering and science, the use of this theorem allows specialists to:

Easily shift the focus on the signal from the time or frequency domain.

Reduce the time wastage on complicated integrals and make multiplication the main focus.

Achieve better performance in solving differential equations.

The ease makes many people say it is a theorem that all students seemed to learn about in different subjects.

The Scope of Convolution Theorem in Real-Life Applications

Numerous fields can make use of the convolution theorem formula flexibility and its benefits. Given below are a few of the most notable ones:

1. Signal Processing

Signals are vital in many industries and need special handling, especially in audio processing, telecommunications, and radio filtering, which requires the use of the contraction theorem. These systems apply theorems to manipulate and analyze the signals.

For Example:

To minimize the disruptive noises during sound transmission, engineers can either use convolution in the time domain or multiplication in the frequency domain.

This principle is the cornerstone of equalizer changes for most music systems.

2. Image Processing

Convolution also aids in image processing in no lesser way. Common practices such as blurring/ sharpening/ edge detecting images require an image to be convolved with a filter kernel to perform these tasks:

The direct convolution with images, called Convolution in the spatial domain, is not ideal for bigger images as it consumes a lot of processing power. Transforming these images into the frequency domain allows for simplified computation through the use of the convolution theorem.

3. Control Systems

Convolution allows you to capture the relationship between signals sent into the system and the responses received from it which is usually done in the case of linear time invariant systems. Using the theorem enables the engineers to:

Make the analysis of the system simpler.

Enhance the accuracy and efficiency of predicting the behavior of the system.

4. Physics and Engineering

Just like in electrical engineering and quantum mechanics, The convolution theorem is fundamental. Its application aids in a variety of tasks from computing impulse responses in circuits to solving physics integral equations, as this theorem allows one to move freely between different domains.

5. Data Analysis and Machine Learning

Modern data science also is aided by the convolution theorem like:

Part of the name and function of certain Neural Networks, specifically Convolutional Neural Networks (CNNs), derives from the convolution operation.

It is common that, in machine learning, algorithms have their computational efficiency enhanced with the use of Fourier based transformation.

6. Statistics and Probability

The convolution of probability distributions appears in statistical analysis as follows:

Addition of Random Variables: If independent random variables are summed, their probability distributions convolve into one resultant probability distribution.

A Step by Step Example

In an attempt to illustrate the theorem, here is a straight forward example that shows how to do it in case of signal processing:

Step 1.

Define the Signals

\( f(t) \): A pulse signal that exists in the time domain.

\( g(t) \): A Gaussian filter.

Step 2.

Fourier Transform Both Signals

Compute the Fourier transforms for \( f(t) \) and \( g(t) \).

Step 3.

Multiply in Frequency Domain

Multiply the functions \( F(\omega) \) and \( G(\omega) \) that are defined in the Fourier transform space.

Step 4.

Apply the Convolution Theorem

Go back to the time domain with the help of inverse Fourier transformation. The obtained value is the convolution result of \( f(t) \) and \( g(t) \) in the time domain.

This workflow is a summary on how the convolution theorem has significantly eased the convolution based tasks.

Paraphrase Everything Using Convolution Theorem, That is, Work Smarter, Not Harder

Convolution theorem is one of the most important of its kind. It enables people who work with engineering, physics, and data sciences to transform time and frequency domains without additional tasks or calculations. Ranging from better audio filter design to even deepening our understanding of neural networks, This simple and profound equivalence is the basis of most modern technologies.

 

 

 

Leave a Reply