The Convolution Theorem

The Convolution Theorem, we know that the Laplace transform of a sum of two functions is the sum of the transforms of those functions, i.e.,

$\mathcal{L}\left\{f\left(t\right)+g\left(t\right)\right\}=\mathcal{L}\left\{f\left(t\right)\right\}+\mathcal{L}\left\{g\left(t\right)\right\}$

On the same analogy we may think of a similar result for the Laplace transform of a product of two functions. But it is not the case; the Laplace transform of a product of two functions is not equal to the product of their transforms, i.c.,
$\mathcal{L}\left\{f\left(t\right)g\left(t\right)\right\}\ne \mathcal{L}\left\{f\left(t\right)\right\}\mathcal{L}\left\{g\left(t\right)\right\}$
However, there is a sort of “generalized multiplication” of two functions called the convolution, whose transform is the product of transforms of the two functions,
$\mathcal{L}\left\{convolution\ of\f\left(t\right)and\g\left(t\right)\right\}=\mathcal{L}\left{f\left(t\right)\right\}\mathcal{L}\left\{g\left(t\right)\right\}=F\left(s\right)G\left(s\right)$

We are interested in it because products of transforms often come up while solving ordinary differential equations, integral equations, etc. We usually know the values of F(s), and G(s), and are interested in finding the value of {latex]\mathcal{L}^{-1}\left\{F\left(s\right)G\left(s\right)\right\}[/latex]. That is, we want to find the function whose transform is the product [F(s) G(s)]. The operation of convolution helps us in this regard and does the needful very conveniently.
The operation of convolution is a very useful concept that has many applications in various fields of engineering. For instance, for any arbitrary input to a time-invariant linear system, convolution is used to obtain the impulse-response of this system.

Convolution of Two Functions (Definition)

If f(t) and g(t) are two piecewise continuous functions, defined on [0, ∞), and of exponential order, then a special product of these functions, denoted by $\left(f\cdot g\right)\left(t\right)$ , called convolution of f(t) and g(t), is defined by either (equivalent) integral,

$\left(f\cdot g\right)\left(t\right)=\int _0^tf\left(t-\tau \right)g\left(\tau \right)d\tau$ (10.1)

$\left(f\cdot g\right)\left(t\right)=\int _0^tf\left(\tau \right)g\left(t-\tau \right)d\tau ,\ \ \ \ t\ge 0$

It is also called the convolution integral.

Properties of the Convolution

The convolution of two functions is not the same as the usual function multiplication, however, it shares many of the properties of the latter operation. The same are summarized below.

If the functions f(t) and g(t) are piecewise continuous on [0, ∞), and of exponential
order, then,

a. $f\cdot g=g\cdot f$ (Commutative Property)

b. $f\cdot \left(g\cdot h\right)=\left(f\cdot g\right)\cdot h$ (Associative Property)

c. $f\cdot \left(g+h\right)=f\cdot g+f\cdot h$ (Distributive Property)

d. $f\cdot 0=0\cdot f=0$ (Zero Multiplication)

Here, we verify the commutative property; proof of the remaining properties may be undertaken easily.

Proof of the Commutative Property of Convolution

The commutative property may be easily proved by change of variable from $\tau \$ to $v=t-\tau$ , in the definition of $f\cdot g$ , i.e.,
$\left(f\cdot g\right)\left(t\right)=\int _0^tf\left(t-\tau \right)g\left(\tau \right)d\tau$ .

Keeping t fixed and letting $v=t-\tau$ , the above integral becomes,
$\left(f\cdot g\right)\left(t\right)=\int _t^0f\left(v\right)g\left(t-v\right)\left(-dv\right)\$
$\left(f\cdot g\right)\left(t\right)=\int _0^tf\left(v\right)g\left(t-v\right)\left(dv\right)\ \ \ \ \$
$\left(f\cdot g\right)\left(t\right)=\int _0^tf\left(v\right)g\left(t-v\right)f\left(v\right)dv\ \ \ \ \$

$\left(f\cdot g\right)\left(t\right)=\left(g\cdot f\right)\left(t\right)$ (by definition of $\left(g\cdot f\right)$ (10.2)

This proves the commutative property of convolution.

Example 10.1

Evaluate $\left(t^2\ \cdot \sin t\right)$ and $\left(\sin t\cdot t^2\right)$ to confirm the equality of these two convolution operations, and hence prove the commutative property of convolution.

Solution

We have,

$\left(t^2\cdot \sin t\right)=\int _0^t\tau ^2\sin \left(t-\tau \right)d\tau$
$\left(t^2\cdot \sin t\right)=\int _0^t\tau ^2\left[\sin t\cos \tau -\cos t\sin \tau \right]d\tau$

$\left(t^2\cdot \sin t\right)=\sin t\int _0^t\tau ^2\cos \tau d\tau -\cos t\int _0^t\tau ^2\sin \tau d\tau$

$\left(t^2\cdot \sin t\right)=\sin t\left[t^2\sin t+2t\cos t-2\sin t\right]-\cos t\left[-t^2\cos t+2t\sin t+2\cos t-2\right]$ (10.3)

And,

$\left(\sin t\cdot t^2\right)=\int _0^t\sin \tau \left(t-\tau \right)^2d\tau$

$\left(\sin t\cdot t^2\right)=\int _0^t\sin \tau \left(t^2-2t\tau +\tau ^2\right)d\tau$

$\left(\sin t\cdot t^2\right)=t^2\int _0^t\sin \tau d\tau -2t\int _0^t\tau \sin \tau d\tau +\int _0^t\tau ^2\sin \tau d\tau$

$\left(\sin t\cdot t^2\right)=2\cos t+t^2-2.$ (10.4)

This example confirms that the convolution operation is commutative. Moreover, it also shows that at times calculating $\ \left(f\cdot g\right)\left(t\right)$ is simpler than calculating $\left(g\cdot f\right)\left(t\right)$ , or vice versa.

Theorem 10.18.1 (Convolution Theorem/Transform of Convolution)

Suppose that f(t) and g(t) are piecewise continuous functions on [0, ∞), and both are of exponential order. Further suppose that $L\left\{f\left(t\right)\right\}=F\left(s\right)$ , and $\mathcal{L}\left\{g\left(t\right)\right\}=G\left(s\right)$ . Then,

$\mathcal{L}\left\{g\left(t\right)\right\}=G\left(s\right)$ (10.3)’

Stated in the inverse form, we can write it as,

$\mathcal{L}^{-1}\left\{F\left(s\right)G\left(s\right)\right\}=\left(f\cdot g\right)\left(t\right)$

Proof

From the definition of the Laplace transform, and the convolution operation we obtain,

$\begin{array}{l}\mathcal{L}\left\{\left(f\cdot g\right)\left(t\right)\right\}=\int _{t=0}^{\infty }e^{-st}\left(f\cdot g\right)\left(t\right)dt\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\int _{t=0}^{\infty }e^{-st}\left(\int _{\tau =0}^tf\left(\tau \right)g\left(t-\tau \right)d\tau \right)dt\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\int _{t=0}^{\infty }\int _{\tau =0}^te^{-st}f\left(\tau \right)g\left(t-\tau \right)d\tau dt\end{array}$

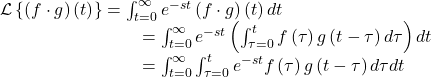
The region of integration in this double integral is the overlapping region defined by,

$\ 0\le t\le \infty ,\ \ \ o\le \tau \le t$

This overlapping region may also be described as,

$0\le \tau \le \infty ,\ \ \ \tau \le t\le \infty$

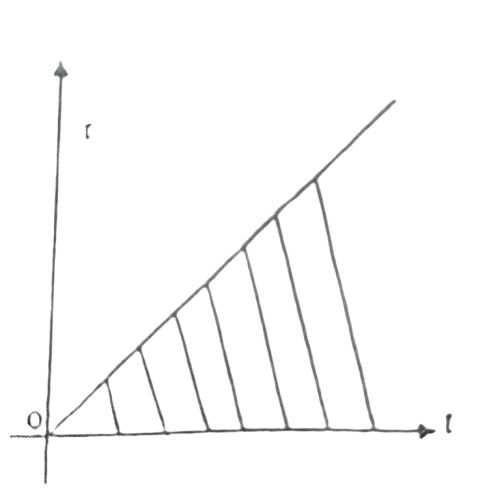
Fig 10.1 Region of Integration

That is, the domain of integration for the above double integral is the entire region lying between $\tau = 0$ and $\tau = t$ . Accordingly, interchanging the order of integration we obtain,

$\mathcal{L}\left\{\left(f\cdot g\right)\left(t\right)\right\}=\int _{\tau =0}^{\infty }\int _{t=\tau }^{\infty }e^{-st}f\left(\tau \right)g\left(t-\tau \right)dtd\tau$

$\mathcal{L}\left\{\left(f\cdot g\right)\left(t\right)\right\}=\int _{\tau =0}^{\infty }e^{-st}f\left(\tau \right)\left[\int _{t=\tau }^{\infty }e^{-s\left(t-\tau \right)}g\left(t-\tau \right)dt\right]d\tau$

$\mathcal{L}\left\{\left(f\cdot g\right)\left(t\right)\right\}=\int _{\tau =0}^{\infty }e^{-st}f\left(\tau \right)\left[\int _{v=0}^{\infty }e^{-sv}g\left(v\right)dv\right]d\tau ,$

(on substituting $t-\tau =v$

$\mathcal{L}\left\{\left(f\cdot g\right)\left(t\right)\right\}=\int _{\tau =0}^{\infty }e^{-st}f\left(\tau \right)\left[\mathcal{L}\left\{g\right\}\right]d\tau$

$\mathcal{L}\left\{\left(f\cdot g\right)\left(t\right)\right\}=\int _{\tau =0}^{\infty }e^{-st}f\left(\tau \right)d\tau \left[\mathcal{L}\left\{g\right\}\right]$

$\mathcal{L}\left\{\left(f\cdot g\right)\left(t\right)\right\}=\mathcal{L}\left\{f\right\}\mathcal{L}\left\{g\right\}$

$\mathcal{L}\left\{\left(f\cdot g\right)\left(t\right)\right\}=F\left(s\right)G\left(s\right)$

which proves the convolution theorem.

Alternate Proof

Again starting from the definition of Laplace Transform we have,

$\begin{array}{l}F\left(s\right)G\left(s\right)=\left[\int _{u=0}^{\infty }e^{-su}f\left(u\right)du\right]\left[\int _{v=0}^{\infty }e^{-sv}g\left(v\right)dv\right]\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\int _{u=0}^{\infty }\int _{v=0}^{\infty }e^{-s\left(u+v\right)}f\left(u\right)g\left(v\right)dvdu\ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\int _{v=0}^{\infty }\int _{u=0}^{\infty }e^{-s\left(u+v\right)}f\left(u\right)g\left(v\right)dudv\ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\int _{v=0}^{\infty }g\left(v\right)\left[\int _{u=0}^{\infty }e^{-s\left(u+v\right)}f\left(u\right)du\right]dv.\end{array}$

To simplify we put $t=u+v$ in the inner integral to get,

$F\left(s\right)G\left(s\right)=\int _{v=0}^{\infty }g\left(v\right)\left[\int _{t=v}^{\infty }e^{-sv}f\left(t-v\right)dt\right]dv.$

Replacing $v$ by $\tau$ , it becomes,

$F\left(s\right)G\left(s\right)=\int _{\tau =0}^{\infty }g\left(v\right)\left[\int _{t=\tau }^{\infty }e^{-sv}f\left(t-\tau \right)dt\right]d\tau .$

Now, as can be seen from Fig. 10.1, the region specified by the above double integral, $0\le \tau \le \infty ,\ \ \tau \le t\le \infty$ is the same as given by $0\le t\le \infty ,\ \ 0\le \tau \le t$ .Therefore, we can write the above integral as,

$F\left(s\right)G\left(s\right)=\int _{t=0}^{\infty }e^{-st}\left[\int _{\tau =0}^tf\left(t-\tau \right)g\left(\tau \right)d\tau \right]dt$

$F\left(s\right)G\left(s\right)=\int _{t=0}^{\infty }e^{-st}\left[f\cdot g\right]dt=\mathcal{L}\left\{\left(f\cdot g\right)\left(t\right)\right\}$

or,

$\mathcal{L}^{-1}\left\{F\left(s\right)G\left(s\right)\right\}=f\left(t\right)\cdot g\left(t\right)$ .

which proves the theorem.

Example 10.2

Evaluate $\left(\cos at\cdot \sin at\right)$

Solution

Using the convolution theorem we obtain,

$\cos at\cdot \sin at=\int _0^t\cos \ a\tau \ \sin \ a\left(t-\tau \right)d\tau$ ,

Employing the trigonometric formula $2\cos A\sin B=\sin \left(A+B\right)-\sin \left(A-B\right),$ we get,

$\cos at\cdot \sin at=\frac{1}{2}\left[\int _0^t\ \sin \ at-\sin \left(2a\tau -at\right)\right]d\tau \$

$\cos at\cdot \sin at=\frac{1}{2}\left[\left|\tau \sin at\right|_{\tau =0}^t+\frac{1}{2a}\cos \left|\left(2a\tau -at\right)\right|_{\tau =0}^t\right]$

$\cos at\cdot \sin at=\frac{1}{2}t\sin at.\$

Note

Convolution often provides a convenient way to evaluate inverse Laplace transform instead of resorting to the partial fraction.

Example

Evaluate $\mathcal{L}^{-1}\left\{\frac{2}{s^2\left(s^2+1\right)}\right\}$

Solution

It may be seen that if we were to evaluate the given inverse Laplace transform by resolving $\frac{2}{s^2\left(s^2+1\right)}$ into partial fractions, we would be required to decompose it as,

$\frac{2}{s^2\left(s^2+1\right)}=\frac{A}{s}+\frac{B}{s^2}+\frac{Cs+D}{s^2+1}$

which would be quite cumbersome. However, in such cases the operation of convolution makes the job very easy, as may be seen below:

$\mathcal{L}^{-1}\left\{\frac{2}{s^2\left(s^2+1\right)}\right\}=2\mathcal{L}^{-1}\left\{\frac{1}{s^2}\right\}+\mathcal{L}^{-1}\left\{\frac{1}{s^2+1}\right\}$