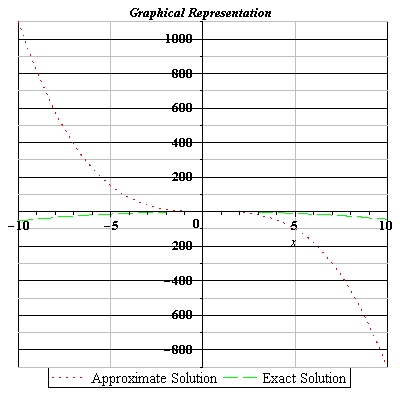
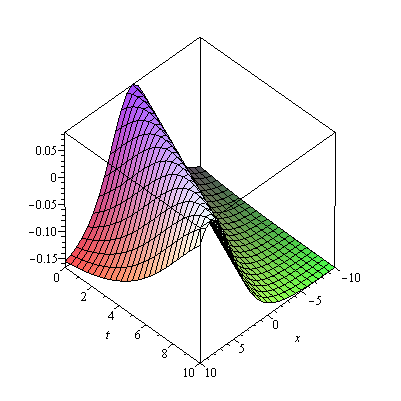
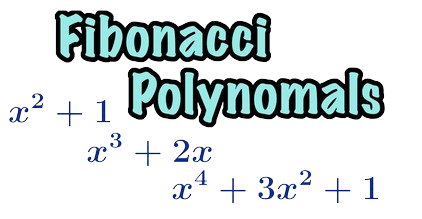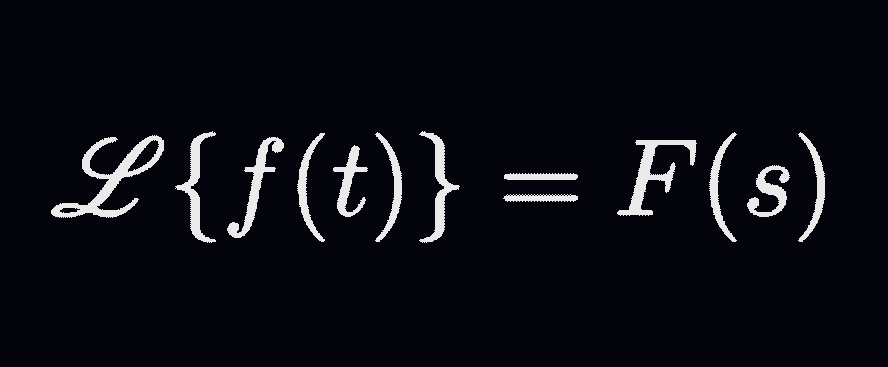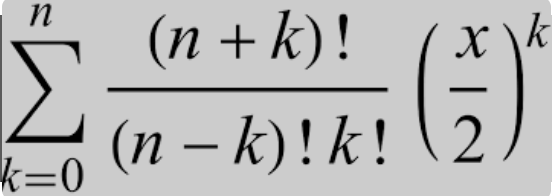Applications of Gegenbauer Polynomials Method,we develop a new algorithm for solving linear and nonlinear integral equations using Galerkin weighted residual numerical method with Gegenbauer polynomials. Gegenbauer polynomials [1] is given as (3.96) , . […]
Laplace Transforms
Laplace Transforms acquired a new importance when the English Electrical Engineer Oliver Heaviside(1850-1925 AD) made use of them in operational calculus(devised by him) and for the solution of ordinary differential equations with constant coefficients. The […]
Solitary Wave Solution
Solitary Wave Solution has been developed, for regularized long width equation in which the auxiliary equation different from traditional (G`/G)-Expansion Method. This method is more general and very simple. This method is more reliable and […]
Monic Wavelet Method
Monic Wavelet Method, is a relatively new and emerging area in mathematical research. As a powerful tool, wavelets have been extensively used in signal processing, numerical analysis and many other areas. Wavelets theory is a […]
Appell Polynomials Method
Appell Polynomials Method,we develop a new algorithm for solving linear and nonlinear integral equations using Galerkin weighted residual numerical method with Appell polynomials [1]. Appell polynomials is given as (3.314) . . […]
Bell Polynomials Method
Bell Polynomials Method ,we develop a new algorithm for solving linear and nonlinear integral equations using Galerkin weighted residual numerical method with Bell polynomials [1]. Bell polynomials is given as […]
Bessel Polynomial Method
Bessel Polynomial Method,we develop a new algorithm for solving linear and nonlinear integral equations using Galerkin weighted residual numerical method with Bessel polynomials [1]. Bessel polynomials is given as 3.8.1 Methodology Definition 3.7. Consider the integral […]
Charlier Polynomials Method
Charlier Polynomials Method, we develop a new algorithm for solving linear and nonlinear integral equations using Galerkin weighted residual numerical method with Charlier’s polynomials [1] is given as 3.7.1 Methodology Definition 3.5. Consider the integral […]
Gegenbauer Polynomials Method
Gegenbauer Polynomials Method is a new algorithm for solving linear and nonlinear integral equations using Galerkin weighted residual numerical method with Gegenbauer polynomials. Gegenbauer polynomials [1] is given as 3.6.1 Methodology Definition 3.3. Consider the […]
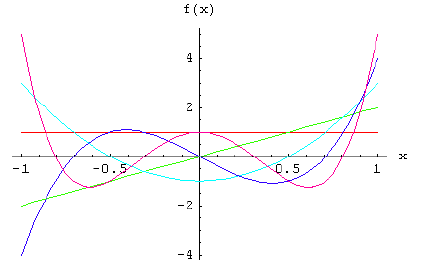
Fibonacci Polynomials Method
Fibonacci Polynomials Method develop a new algorithm for solving linear and nonlinear integral equations using Galerkin weighted residual numerical method with Fibonacci polynomials [1]Fibonacci polynomials is given as 4.1.1 Methodology Definition 4.1. Consider the integral […]