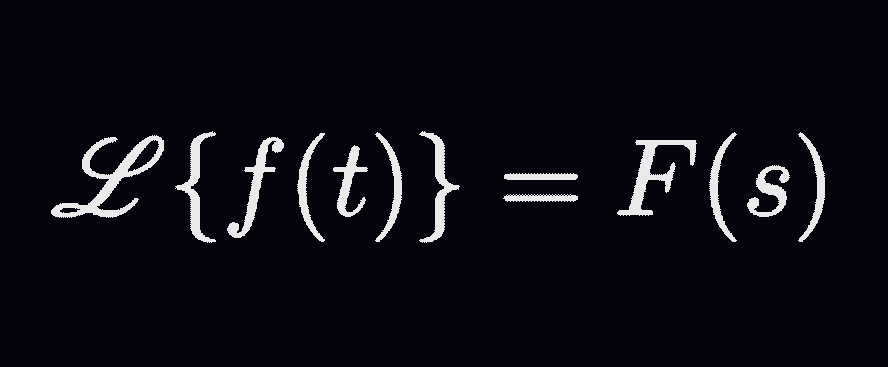Laplace Transforms acquired a new importance when the English Electrical Engineer Oliver Heaviside(1850-1925 AD) made use of them in operational calculus(devised by him) and for the solution of ordinary differential equations with constant coefficients. The methods of Laplace transforms enabled him to solve some important practical problems that could not be dealt with by the classical methods. For instance we can solve differential equation representing the motion of a spring driven by a periodic or constant force, by usual methods, however these methods no more help if the force is impulsive. In other words, the usual classical methods can solve an ordinary differential equation ![]() , when
, when ![]() is continuous but these methods become ineffective and of no use if
is continuous but these methods become ineffective and of no use if ![]() is discontinuous or piece-wise continuous. In such cases the methods of Laplace transforms come to our rescue and resolve the problems.
is discontinuous or piece-wise continuous. In such cases the methods of Laplace transforms come to our rescue and resolve the problems.
Initial value and boundary value problems can also be solved with the help of the Laplace transforms
- input signal
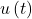
- system
- output signal
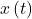
The laws controlling a system’s behavior serve as the foundation for the correlation between its input and output. A linear differential equation with constant coefficients connects the output to the input if the system is linear and time-invariant. In actuality, it is an initial value problem that the Laplace transform approach may resolve.
Definition of the Laplace Transforms
One type of integral transform is the Laplace transform. It takes a function f(t), of one variable t (time) into a function ![]() of another variable s (frequency). Let f(t) be a given function defined for all
of another variable s (frequency). Let f(t) be a given function defined for all ![]() . The Laplace transform of f(t) is denoted by
. The Laplace transform of f(t) is denoted by ![]() or
or ![]() being Laplace transform operator. It is defined as:
being Laplace transform operator. It is defined as:
![]() (1)
(1)
Example 1:
Determine the Laplace transformations of, ![]()
Solution
Using Eq. (1) we obtain,
For ![]()
For ![]()
For ![]()
![]()
![Rendered by QuickLaTeX.com f\left(t\right)=\cos at,\ \mathcal{L}\left\{f\left(t\right)\right\}=\int _0^{\infty }e^{-st}\cos atdt=\left[\frac{e^{-st}\left(-s\ \cos at+a\sin at\right)}{s^2+a^2}\right]_0^{\infty }= \frac{s}{s^2+a^2}](https://mathematicsglobe.com/wp-content/ql-cache/quicklatex.com-a9e0f81a434046d6ffc1f028199ac802_l3.png)
Enough Prerequisites for the Laplace Transform to Exist
The integral
![]()
defining the Laplace transform of a function ![]() may not always converge.For instance,
may not always converge.For instance,
![]() and
and ![]() do not exist. Sufficient conditions that guarantee the existence of
do not exist. Sufficient conditions that guarantee the existence of ![]() are as under:
are as under:
a. f is piecewise continuous on ![]() , and
, and
b. f is of exponential order for ![]() .
.
A function ![]() is piecewise continuous on
is piecewise continuous on ![]() , if in any interval
, if in any interval ![]() there are at most a finite number of discontinuous at points
there are at most a finite number of discontinuous at points ![]() and f is continuous in open intervals
and f is continuous in open intervals ![]() .An example of piecewise continuous function is as under:
.An example of piecewise continuous function is as under:
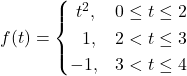
A function ![]() is said to be of exponential order if there exist numbers
is said to be of exponential order if there exist numbers ![]() , M>0 and t>0, such that
, M>0 and t>0, such that ![]() the graph of
the graph of ![]() does not grow faster than the graph of
does not grow faster than the graph of ![]() . For example,
. For example, ![]() are all of exponential order for t>0, since we have, respectively
are all of exponential order for t>0, since we have, respectively
![]()
On the other hand ![]() is not of exponential order, since it grows faster than
is not of exponential order, since it grows faster than ![]() for any choice of
for any choice of ![]() and .
and .
Theorem (Existence of Laplace Transform)
Let ![]() be piecewise continuous on the interval
be piecewise continuous on the interval ![]() and of exponential order for
and of exponential order for ![]() , (i.e., there exist
, (i.e., there exist ![]() , such that
, such that ![]() for all
for all ![]() ).Then
).Then ![]() exists for
exists for ![]() .
.
Proof
Since, ![]() is piecewise continuous on
is piecewise continuous on ![]() and of exponential order for
and of exponential order for ![]() , i.e,
, i.e, ![]()
![]()
![]()
This demonstrates the existence of the function’s piecewise continuous and exponentially ordered Laplace transforms. It should be mentioned, nevertheless, that these prerequisites are adequate—not essential—for a Laplace transform to exist. For example, the function ![]() is not piecewise continuous on the interval
is not piecewise continuous on the interval ![]() because of its behaviour at t=0, but its Laplace transform exists(see example below)
because of its behaviour at t=0, but its Laplace transform exists(see example below)
Example 2:
Determine the Laplace transform of ![]()
Solution
![]() (2)
(2)
Let ![]() , i.e.,
, i.e., ![]() . Differentiating the former equation w.r.t t we get,
. Differentiating the former equation w.r.t t we get,
![]() i.e.,
i.e., ![]()
Therefore, equation (2) becomes
![]()
But ![]() .
.
Therefore
![]()
Linearity of the Laplace Transform
The Laplace transform is a linear operator. This property of the former is stated as under:
If f(t) and g(t) are any two functions having Laplace transforms, and if a and b are any constants, then
Accordingly we say that Laplace transform operator ![]() is a linear operator. Using the Laplace transform definition, the aforementioned may be easily demonstrated as follows:
is a linear operator. Using the Laplace transform definition, the aforementioned may be easily demonstrated as follows:
![Rendered by QuickLaTeX.com \begin{array}{l}\mathcal{L}\left\{af\left(t\right)+bg\left(t\right)\right\}=\int _0^{\infty }\left[af\left(t\right)+bg\left(t\right)\right]e^{-st}dt\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\int _0^{\infty }af\left(t\right)e^{-st}+bg\left(t\right)e^{-st}dt\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =a\int _0^{\infty }f\left(t\right)e^{-st}dt+b\int _0^{\infty }g\left(t\right)e^{-st}dt\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =a\ \mathcal{L}\left\{f\left(t\right)\right\}+b\mathcal{L}\left\{g\left(t\right)\right\}\end{array}](https://mathematicsglobe.com/wp-content/ql-cache/quicklatex.com-2d4967e9c2e295725f256a0dac1db723_l3.png)
The First Shift Property of Laplace Transform
The First shift property of Laplace transform sometimes referred to as Exponential Modulation Theorem.
The First Shift Theorem
If f(t) is a function having Laplace transform ![]() , then
, then
![]()
Proof
Using the definition of Laplace transform we get,
![]() (3)
(3)
Now, by definition
![]() (4)
(4)
We see that integral (3) is exactly the same as integral (4), the Laplace transform of f(t) , with (s-a) in place of s. Thus integral (3) gives,
![]() .
.
![]() .
.
Therefore, if we already know ![]() , we can easily compute
, we can easily compute ![]() by shifting or translating
by shifting or translating ![]() .If we consider the graphs of
.If we consider the graphs of ![]() and
and ![]() , we see that the graph of
, we see that the graph of ![]() is the graph of
is the graph of ![]() shifted on the s-axis by an amount of
shifted on the s-axis by an amount of ![]() units to the right.
units to the right.
Example 3:
Evaluate ![]()
Solution
By definition of Laplace transform,
![]()
![]()
![]()
![]()
Now we solve this problem by First Shift Theorem. We know that
![]()
Now, by the First Shift Theorem, if
![]() .
.