Introduction of Novel Operational Matrices

Introduction of Novel Operational Matrices, may be modified to examine the solution to more diverse problems of a physical nature in intricate geometries. Research was conducted to verify the consistency and aid the mathematical structure of the algorithm.

Abstract

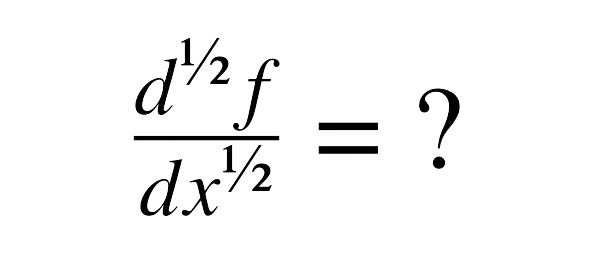
Finding solutions for the multi-dimensional delay problems of fractional-order appearing in mathematics, physics, and engineering has become a difficult problem to research. This article demonstrates the creation and successful application of an efficient fully spectral operational matrices-based scheme for stable solutions of time-fractional delay differential equations (DDEs). Proposed novel operational matrices for fractional-order integration $I^v$ and $D^v$ were created using shifted Gegenbauer polynomials. A number of ordinary and partial DDEs of fractional order are considered to demonstrate the reliability, efficiency and applicability of the proposed method. To help with taking the delay term in DDEs, a new delay operational matrix $\Theta _b^a$ is created with the use of shifted Gegenbauer polynomials. The devised algorithm transforms the problem of the system under consideration into a set of algebraic problem which is far less complicated. Effective analytic solutions to these problems are obtained, and broad ranging comparative analyses are detailed that show the proposed computational scheme is robust, precise and well suited for exploring the solutions of the problems referenced. In this work, we give a bound analysis in detail.

Mathematics, especially the study of Differential Eqn. assumes constant real number order derivatives and now it is well known that fractional derivatives has been one of the most interesting and another branch of the Fractional Calculus (FC) because of its wide application in engineering,, stochastic, biological and industrial systems [1,2]. This particular area of research appears to have matured from a pair of well-known mathematicians (Hospital and Leibniz); it is still debated and told that it can also be used to perform simulations of both simple and complex systems which have viscoelastic behaviors. Several experts have offered comprehensive definition to calculate the fractional-order derivative [3,4]. One can already observe that the set of functional differential equations (FDEs) are extremely useful for other areas of disciplines such as thinking, economics, signal processing, filtering, electrical engineering, electroanalytical chemistry, solid state physics and statistical mechanics. Which can be seen in refs. [5–11]. It is a well-known fact that fractional differential equations also arise in the physical-chemistry of chemical symmetry regarding mass transport suitable for dissolution concentration from donor to acceptor type.

The aforementioned applications within both science and engineering helped scientists design computer models to replicate the extraordinary wonders of nature. Over the past decade, a remarkable variety of phenomena has been created in a computer. Following development of these models, the next and most crucial step was to find an optimal solution to the identified problems. This was most challenging task for FDEs, however many analytical and numerical approaches have been abundantly used to estimate the solution of the problem at hand [12–16]. Ul Hassan [17] proposed a procedure based on the soliton concept to analyze the effect of fractional-order (biological population) differential equations. Shah et al. [18] studied the heat transfer for a second grade fluid over an oscillating vertical plate. A detailed investigation of fractional and variable order DDEs has recently been done by Aguilar et al. [19]. In that paper, these authors solved the problem by artificial neural networks. The equations of delay differential [20,21] are known with fractional order (FDDE) derivatives and are stated as,

$\ _0^CD_t^vy\left(t\right)=F\left(y\left(t\right)\right)+\beta _1y\left(at-b\right)+\beta _2y\left(t\right)+G\left(t\right),$ (1)

In Eq. (1), y(t) is dependent variable, F is the nonlinear operator and ν is fractional-order derivative with 0 < ν ≤ 1.
Furthermore, $\beta _i\ ,\ i=1,2,\ a\ \ne 0,\ b$ are arbitrary constants which is different for different kinds of delay differential problems. $y\left(at-b\right)$ and $G\left(t\right)$ are delay function and nonhomogeneous function of the expression (1) respectively. The suitable initial condition is given as,

$y\left(t\right)=\phi \left(t\right),\ t\ge 0$ (2)

The research community already feels daunted because of the multi-disciplinary relevance of science and technology like chemistry, finance, and physics[22]. In this regard Daftardar-Gejji & Jafari developed [23] presented an efficient new iterative scheme to search numerical solution of the problem formulated in (1)-(2). Daftardar-Gejji et al’s.[24] claimed to have developed a new predictor-corrector technique for the determination of fractional order delay differential equations. In this article, it is presented that the new technique is superior in accuracy and time efficiency when compared to other techniques. Research observations now reveal that the time-fractional delay partial differential equations dealing with the modeling of dynamics of populations structured with respect to size of cell, specimen age, and maturation level, etc. are becoming common place. [25,26].The general form of time-fractional delay partial differential equations defined in $0\le x\le L,\ 0\le t\le T\ ,\ 0<v\le 1$

$_0^CD_t^vu\left(x,t\right)+\mu _{10}^CD_t^vy\left(t\right)u\left(x,a_1t+b_1\right)$

$=\mu _2\ \frac{\partial ^2u}{\partial x^2}+\mu _3\ \frac{\partial ^2}{\partial x^2}u\left(x,a_2t+b_2\right)+\mu _4u\left(x,a_3t+b_3\right)+\mu _5u\left(a_4x+b_4,t\right)+\mu _6u\left(a_5x+b_5,a_6t+b_6\right)+\mu _7F\left(u\left(x,t\right)\right)+f\left(x,t\right).$ (3)

Conditions subject to above problems are given as

$u\left(x,0\right)=\alpha \left(x\right)$ ,

$u\left(0,t\right)=\beta _1\left(t\right),\ \ u\left(L,t\right)=\beta _2\left(t\right)$ .(4)

where $\mu _{i\ },\ a_j,\ b_j$ for $i=1,2,...,7\ \ j=1,2,...,6$ are constants, F is nonlinear operator and $f\left(x,t\right)$ is a source term.

Solodushkina et al. [27] proposed an efficient scheme based on finite difference method to study the stable solution of the first order delay partial differential equation which is often encountered in the modeling of the structured cell populations dynamics with respect to maturity and age levels. Zhang and Zhang [28] deals with the neutral delay parabolic differential equations using a new fourth order stable implicit compact difference algorithm. In this article, different type of Richardson extrapolation techniques are used to improve the accuracy of the temporal variable. Niu et al. [29] devised a new collocation reproducing kernel technique aimed at solving the delay heat conduction model. They present several test problems to demonstrate the efficacy and accuracy of their approach.

The application of orthogonal basis polynomials, including, but not limited to,the Haar, Chebyshev, Laguerre, Gegenbauer, Legendre, and Laurent have led to advancements in various branches of science [30-36]. Heydari et al. [37] offered the numerical results of a class of fractional order partial differential equations. They used a polynomial based scheme with Dirichlet boundary conditions. There’s a modified form of wavelet transform which is based on Chebyshev polynomials for a fractional order delay equation that can be found in refs. [38]. The methods provided recently by Usman et al. [39, 40] have been shown to be correct, providing answers to unsure results because they improved the accuracy and performed fewer operations on the computational facility at a given level. With such techniques, they resolved two challenging problems; one involves the fractional differential equations with variable order [39] and the other is a fluid problem [40], which consists of highly and nonlinearly coupled differential equations as problems. Other methods can be seen in [41-44].

The shifts of origin concepts are further applied to Gegenbauer polynomials and constructed shifted Gegenbauer polynomials. With the aid of shifted Gegenhauer monomials, new operational matrices for fractional order integration $I^v$ and differentiation $D^v$ have been developed. To enhance the accuracy and efficiency of the method, novel operational matrix is introduced $\Theta _b^a$ to replace the delay terms that are often encountered in DDEs. Through these operational matrices a procedure for fractional-order delay differential equation is devised which is in fact main contribution of this article. The advancements and applications of this framework with respect to the literature are non-existent. With the aid constructed framework, the delay differential equation is transformed into a system of algebraic equations through the methodology that has been devised. To validate the accuracy of the method, comparisons among the evaluated solution obtained from the proposed method and the exact and published results of the problem are provided. It has been established that this is a precise, efficient and suitable method to solve linear and nonlinear delay differential equations of fractional-order, and it has further scope to be the significant finding for nonlinear fractional order problems.