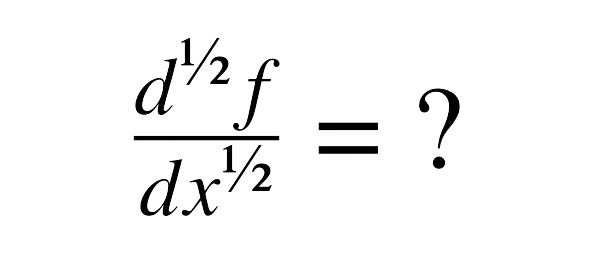
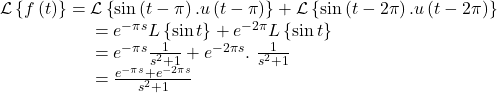Initial Value Problems are solved using the Laplace Transform Method

Initial Value Problems are solved using the Laplace Transform Method, as mentioned earlier, the Laplace transform method is very convenient way of solving ordinary differential equations in general and those with constant coefficients in particular. The advantage of this method is that it replaces differential equations (in variable t) by an algebraic equation (in variable s), which is much easier to solve. After having solved the latter by algebraic rules, the inverse Laplace transform enables us to obtain the solution of the given differential equation in terms of the original variable t.
Initial value problems are solved using the Laplace transform method, where in the initial conditions are automatically included. This contrasts with the usual classical approach in which the general solution of a differential equation comprises the complementary function and the particular integral, where in the initial conditions are used to determine the values of the constants of integration associated with the complementary function.

Example 10.1

Solve $y"+4y=16t,\ y(0)=3,\ y^{\prime }(0)=−6.$

Solution

We take Laplace transforms of both sides of the given differential equation. Thus we obtain,
$\mathcal{L}{y"}+4\mathcal{L}{y} = \mathcal{L}{16t}$
We use the formulae: $\mathcal{L}\left\{y′′\right\}=s^2Y(s)−sy(0)-y^{\prime }(0),\ \ \mathcal{L}\left\{y\right\}=Y(s),\mathcal{L}(t)=\frac{1}{s^2}.$

Therefore, the above equation becomes,

$[s^2Y(s)-sy(0)-y^{\prime }(0)]+4Y(s)=16\left(\frac{1}{s^2}\right).$

Thus using the given initial conditions we obtain,

$[s^2Y(s)-3s+6]+4Y(s)=\frac{16}{s^2},$

i.e.,

$(s^2+4)Y(s)=3s-6+\frac{16}{s^2}$

or,

$Y\left(s\right)=\frac{3s-6}{s^2+4}+\frac{16}{s^2\left(s^2+4\right)}$

$=\frac{3s}{s^2+4}-\frac{6}{\left(s^2+4\right)}+\frac{16}{4}\left(\frac{1}{s^2}-\frac{1}{s^2+4}\right)$

$=\frac{3s}{s^2+4}-\frac{10}{\left(s^2+4\right)}+\frac{4}{s^2}$

Therefore, by taking the inverse Laplace transform of both sides we obtain,

$y\left(t\right)=3\mathcal{L}^{-1}\left\{\frac{s}{s^2+4}\right\}-5\mathcal{L}^{-1}\left\{\frac{2}{s^2+4}\right\}+4\mathcal{L}^{-1}\left\{\frac{1}{s^2}\right\}$

But we know that,

$\mathcal{L}\left\{\cos 2t\right\}=\left\{\frac{s}{s^2+4}\right\},\mathcal{L}\left\{\sin 2t\right\}=\frac{2}{s^2+4},\mathcal{L}\left\{t\right\}=\frac{1}{s^2}\ \$

Therefore, the solution of the given differential equation is,

$\ y\left(t\right)=3\cos 2t-5\sin 2t+4t$

Example 10.2

Solve $\ y"+y=16\cos t,\ \ \ y(0)=0,y^{\prime }(0)=0.$

Solution

Taking Laplace transform of both sides the given equation can be written as,
$\mathcal{L}{y"}+L{y} = 16 L{cost}$

or,

$\ \ \ \ [s^2Y(s)-sy(0)-y^{\prime }(0)]+Y(s)=\frac{16s}{(s2+1)}.$

By using the initial conditions it becomes,

$s^2Y(s)+Y(s)=\frac{16s}{(s^2+1)}$

Thus,

$Y\left(s\right)=\mathcal{L}\left\{Y\left(t\right)\right\}=\frac{16s}{\left(s^2+1\right)^2}$

Taking inverse Laplace transform of both sides we get,

$\ y\left(t\right)=8\mathcal{L}^{-1}\left\{\frac{2s}{\left(s^2+1\right)^2}\right\}$

But we know that,

$\mathcal{L}\left\{t\sin kt\right\}=\frac{2ks}{\left(s^2+k^2\right)^2},\ s>0.$

Thus we get the solution as,

$y(t)=8t\sin t.$

Example 10.3

Solve, $y"+2y^{\prime }+5y=0,y(0)=3,y^{\prime }(0)=-7.$

Solution

Taking Laplace transform of both sides of the given equation we get,

$[s^2Y(s)-sy(0)-y^{\prime }(0)]+2\left\{sY(s)-y(0)\right\}+5Y(s)=0.$

Using the initial conditions this equation becomes,

$[s^2Y(s)-3s+7]+2sY(s)-6+5Y(s)=0.$

i.e.,

$Y(s)(s^2+2s+5)=3s-1.$

Thus,

$Y\left(s\right)=\frac{3s-1}{s^2+2s+5}=\frac{3\left(s+1\right)-4}{\left(s+1\right)^2+4}=3\left[\frac{\left(s+1\right)}{\left(s+1\right)^2+4}\right]-2\left[\frac{2}{\left(s+1\right)^2+4}\right].$

But we know that,

$\mathcal{L}^{-1}\left\{\frac{s}{s^2+4}\right\}=\cos 2t,\mathcal{L}^{-1}\left\{\frac{\left(s+1\right)}{\left(s+1\right)^2+4}\right\}=e^{-t}\cos 2t,$

$\mathcal{L}^{-1}\left\{\frac{s}{s^2+4}\right\}=\sin 2t,\mathcal{L}^{-1}\left\{\frac{2}{\left(s+1\right)^2+4}\right\}=e^{-t}\sin 2t,$

Therefore, taking the inverse Laplace transform of the above equation we obtain the solution of the given differential equation as,

$y\left(t\right)=e^{-t}\left[3\cos 2t-2\sin 2t\right]$

Example 10.4

Solve $\ y"-3y^{\prime }+2y=12e",\ y(0)=1,\ y^{\prime }(0)=0.$

Solution

Taking Laplace transform of both sides we can write the given equation as,

$\ \left[s^2Y\left(s\right)-sy\left(0\right)-y^{\prime }\left(0\right)\right]-3\left[sY\left(s\right)-y\left(0\right)\right]+2Y\left(s\right)=\frac{12}{s-4}$

Using the initial conditions it becomes,

$\ \left[s^2Y\left(s\right)-s\right]-3\left[sY\left(s\right)-1\right]+2Y\left(s\right)=\frac{12}{s-4},$

i.e.,

$Y\left(s\right)\left(s^2-3s+2\right)=s-3+\frac{12}{s-4}$ .

Thus,

$\ Y\left(s\right)=\frac{s^2-7s+24}{\left(s-1\right)\left(s-2\right)\left(s-4\right)}$

Now, we resolve the term on the right into partial fractions. We let,

$\frac{s^2-7s+24}{\left(s-1\right)\left(s-2\right)\left(s-4\right)}=\frac{A}{s-1}+\frac{B}{s-2}+\frac{C}{s-4}$

or,

$s^2-7s+24=A\left(s-2\right)\left(s-4\right)+B\left(s-1\right)\left(s-4\right)+C\left(s-1\right)\left(s-2\right)$

To find A we put s-1 = 0, i.e., s = 1 in the above equation. Thus we get, 18 = A (3), i.c.,
A = 6.
Similarly, to find B and C, we put s = 2, and s = 4 respectively in the above equation.
Accordingly we obtain, B =-7, and C = 2. Thus we get,

$Y\left(s\right)==\frac{6}{s-1}-\frac{7}{s-2}+\frac{2}{s-4}.$

Taking the inverse Laplace transform of both sides we get,

$y\left(t\right)=6\mathcal{L}^{-1}\left(\frac{1}{s-1}\right)-7\mathcal{L}^{-1}\left(\frac{1}{s-2}\right)+2L^{-1}\left(\frac{1}{s-4}\right)$

Therefore,

$\ y\left(t\right)=6e^t-7e^{2t}+2e^{4t}$ .

Example 10.5

Solve $y"+2 y'+y=1, y(0) = 2, y' (0)=-2$

Solution

Taking Laplace transform of both sides of the given equation we obtain,

$\left[s^2Y\left(s\right)-sy\left(0\right)-y^{\prime }\left(0\right)\right]+2\left[sY\left(s\right)-y\left(0\right)\right]+Y\left(s\right)=\frac{1}{s}$

Using the initial conditions this equation becomes,

$\left[s^2Y\left(s\right)-2s+2\right]+2\left[sY\left(s\right)-2\right]+Y\left(s\right)=\frac{1}{s}$

or,

$Y\left(s\right)\left(s^2+2s+1\right)=\frac{1}{s}+2s+2=\frac{2s^2+2s+1}{s}$

or,

$Y\left(s\right)=\frac{2s^2+2s+1}{s\left(s^2+2s+1\right)}=\frac{2s^2+2s+1}{s\left(s+1\right)^2}.$

Resolving the right hand side expression into partial fractions we obtain,

$Y\left(s\right)=\frac{1}{s}+\frac{1}{s+1}-\frac{1}{\left(s+1\right)^2}.$

Taking the inverse Laplace transforms of both sides we get the solution of the given
differential equation as,

$y\left(t\right)=1+e^{-t}-te^{-t}.$

The Delayed Function

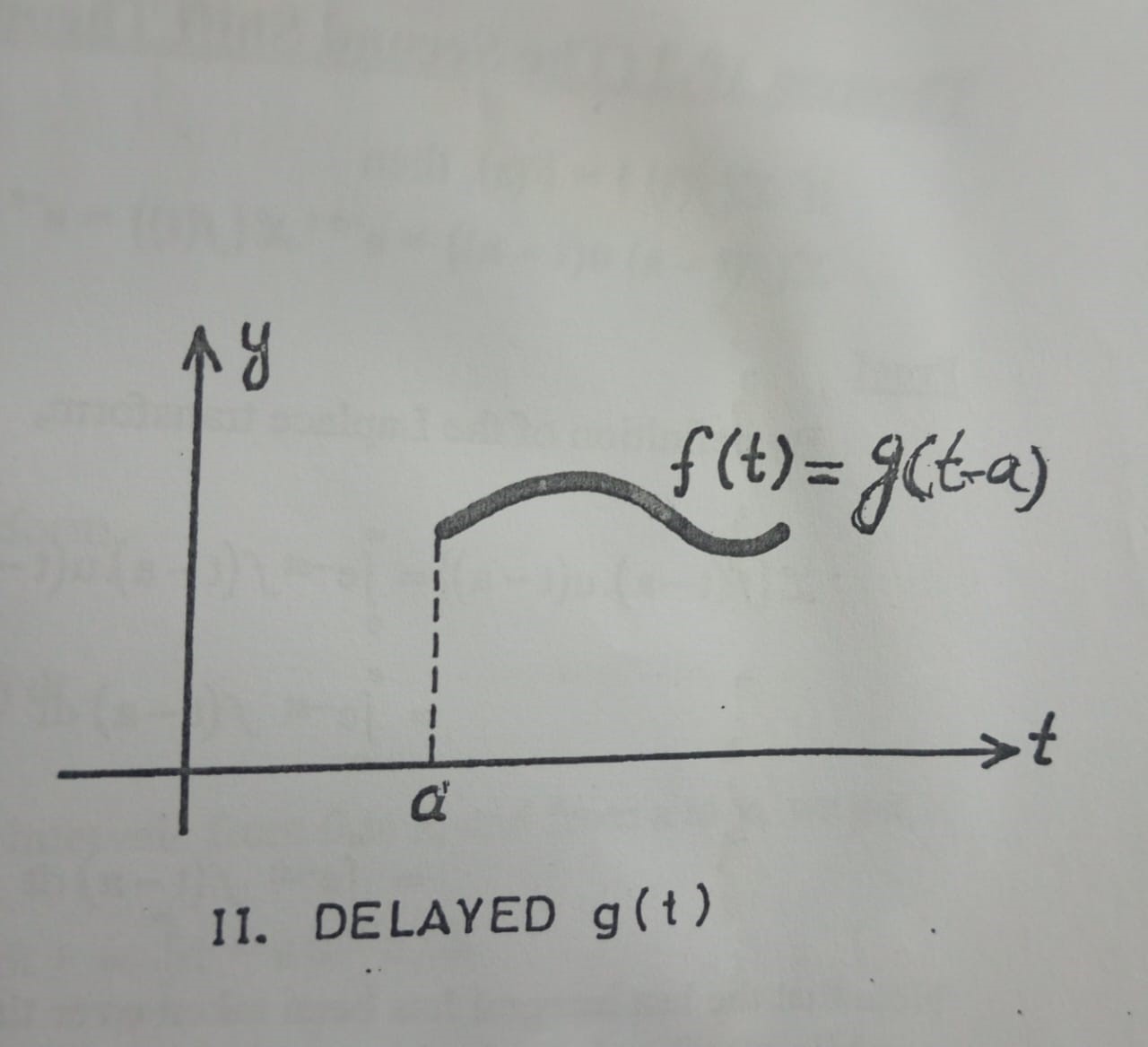
It is often required to translate or shift a given function g(t) to the right by ‘a‘ units and then replace the function by zero to the left of ‘a‘. For instance, if we translate a function g(t), shown in Fig 1 (i), to the right by ‘a‘ units and then replace the function by zero to the left of ‘a‘, the graph of the new function f(t), or delayed g(t) would look like the graph in Fig 1(ii). Mathematically, we could represent such a delayed function g(t) as,

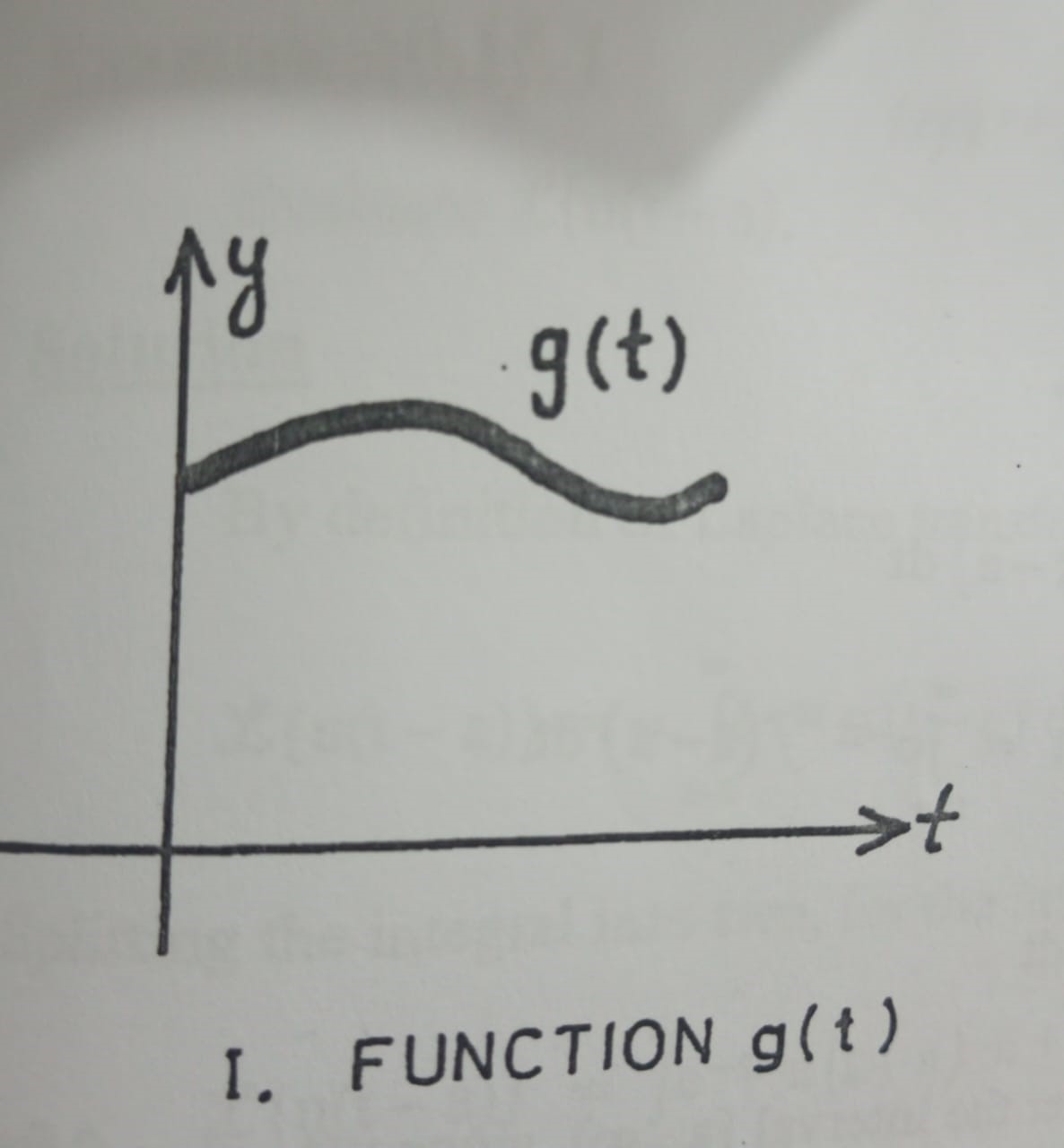
$f\left(t\right)=\left\{\begin{matrix}0,&t<a\\ g\left(t-a\right),\ \ \ \ \ \ &t>a\end{matrix}\right\}$

Fig 1(i)

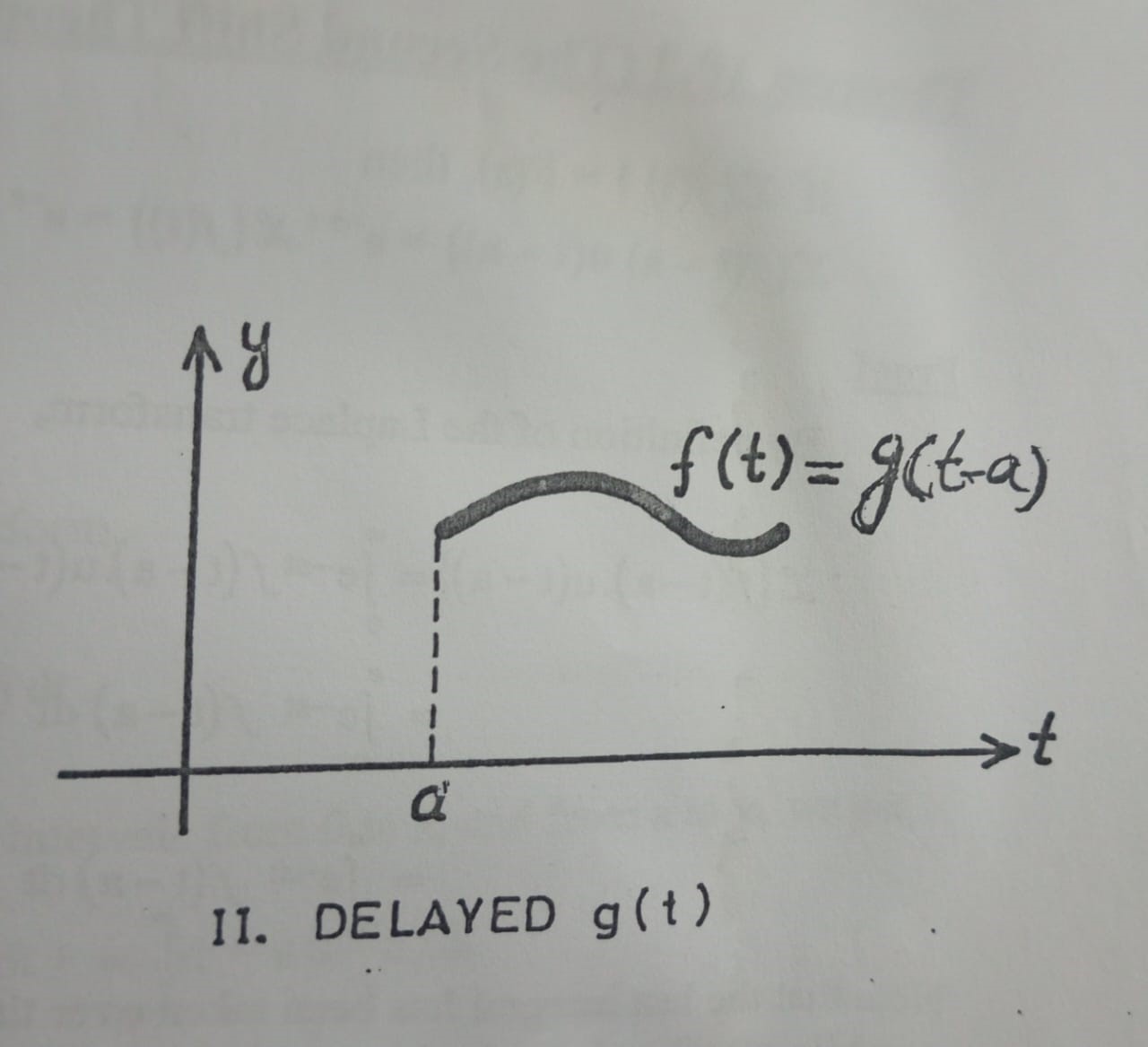
Fig 1(ii)

Example 10.1 (Representing Delayed Function)

Represent mathematically the delayed function obtained when the graph of g(t) =t² is translated 1 unit to the right and then truncated to the left of 1.

Solution

If we translate the given function g(t) to the right by 1 unit, then this function would become [latexg\left(t-1\right)=\left(t-1\right)^2[/latex]. Accordingly the delayed function would be,
0,

$f\left(t\right)=\left\{\begin{matrix}0,&\ \ \ t<1\\ \left(t-1\right)^2,&\ \ \ t>1\end{matrix}\right\}$ (10.1)

Hence, using the formula for piece-wise defined function,the above function can be written in the compact form as,

$f\left(t\right)=f_1\left(t\right)-f_1\left(t\right).u\left(t-a\right)+f_2\left(t\right).u\left(t-a\right)$

$\ f\left(t\right)=0-0.u\left(t-1\right)+\left(t-1\right)^2.u\left(t-1\right)/latex] [latex]f\left(t\right)=\left(t-1\right)^2.u\left(t-1\right)$ (10.2)

Laplace Transform of Delayed Functions

For many problems it is required to find the Laplace transform of the delayed function, $f\left(t-a\right).u\left(t-a\right)$ , we can find this transform directly from the definition of the Laplace transform, as enunciated in the following theorem.

Theorem (The Second Shift Theorem; t-Shifting)

If $L\left\{f\left(t\right)\right\}=F\left(s\right)$ ,

then

$L\left\{f\left(t-a\right)\right\}u\left(t-a\right)=e^{-as}F\left(s\right)$ (10.3)

Proof

By definition of the Laplace transform,

$\mathcal{L}\left\{f\left(t-a\right).u\left(t-a\right)\right\}=\int _0^{\infty }e^{-st}f\left(t-a\right).u\left(t-a\right)dt$

$\mathcal{L}\left\{f\left(t-a\right).u\left(t-a\right)\right\}=\int _{t=0}^ae^{-st}f\left(t-a\right)dt=\int _{t=a}^{\infty }e^{-st}f\left(t-a\right)dt$

$\mathcal{L}\left\{f\left(t-a\right).u\left(t-a\right)\right\}=\int _{t=a}^{\infty }e^{-st}f\left(t-a\right)dt$

Note that the last integral has been taken over the interval [a, ∞), since u(t-a) = 0 for t< a, while u(t-a) = 1 on the interval [a, ∞). On substituting v=t-a in the above integral we obtain,

$\mathcal{L}\left\{f\left(t-a\right)u\left(t-a\right)\right\}=\int _{v=0}^{\infty }e^{-\left(v+a\right)}f\left(v\right)dv$

$\mathcal{L}\left\{f\left(t-a\right)u\left(t-a\right)\right\}=e^{-as}\int _{v=0}^{\infty }e^{-vs}f\left(v\right)dv=e^{-as}F\left(s\right)$

i.e.,

$\mathcal{L}\left\{f\left(t-a\right)u\left(t-a\right)\right\}=e^{-as}\mathcal{L}\left\{f\left(t\right)\right\}$ (10.4)

Conversely,

$\mathcal{L}^{-1}\left\{e^{-as}F\left(s\right)\right\}=f\left(t-a\right).u\left(t-a\right)$ (10.5)

NOTE:

The above theorem essentially says that,
(i) To find the Laplace transform of the delayed function $f\left(t-a\right).u\left(t-a\right),$ we need to take the transform of f(t) and then multiply the transform by $e^{-as}$

(ii) To find the inverse transform of the function $e^{-as}F(s)$ , we need to suppress the factor $e^{-as}$ and take the inverse transform of F(s), getting f(t); then replace t by (t-a), to get f(t-a), and then multiply by u(t-a).

Example 10.1 (Transform of Delayed Function)

Find the Laplace transform of the function $f\left(t\right)=t^2.\ u\left(t-1\right)$

Solution

To be able to apply Theorem, we need to write the given function in the form f(t-1).u(t-1). We see that, $\left(t-1\ \right)^2=t^2\ -2t+1$ ; as such,

$t^2=\left(t-1\right)^2+2t-1$
$t^2=\left(t-1\right)^2+2\left(t-1\right)-1$

Therefore, the given function can be written as:

$f\left(t\right)=t^2.u\left(t-1\right)=\left\{\left(t-1\right)^2+2\left(t-1\right)\right\}.u\left(t-1\right)$

Accordingly, using Theorem , we get the Laplace transform of ƒ (t) as,

$\mathcal{L}\left\{t^2.u\left(t-1\right)\right\}=\mathcal{L}\left\{\left[\left(t-1\right)^2+2\left(t-1\right)\right].u\left(t-1\right)\right\}$

$\mathcal{L}\left\{\left[\left(t-1\right)^2+u\left(t-1\right)\right]+2\mathcal{L}\left\{\left(t-1\right).u\left(t-1\right)\right\}+\mathcal{L}\left\{u\left(t-1\right)\right\}\right\}$

$=e^{-s}\mathcal{L}\ \left\{t^2\right\}+2e^{-s}\mathcal{L}\left\{t\ \right\}+e^{-s}\mathcal{L}\left\{u\left(t-1\right)\right\}$

$=e^{-s}\left[\frac{2}{s^3}+\frac{2}{s^2}+\frac{1}{s}\right].$

Example 10.2

Find the Laplace transform of

$f\left(t\right)=\left\{\begin{matrix}0,&\ \ \ \ \ \ \ \ \ \ 0<t<\pi \\ -\sin t,&\ \ \ \ \ \ \ \ \ \ \pi <t<2\pi \\ 0,&\ \ \ \ \ \ \ \ \ \ t>2\pi \end{matrix}\right\}=\left\{\begin{matrix}0,&\ \ t<\pi \\ -\sin t,&\ \ \ t>\pi \end{matrix}\right\}+\left\{\begin{matrix}-\sin t,&\ \ t<2\pi \\ \ \ 0,&\ \ \ t>2\pi \end{matrix}\right\}$

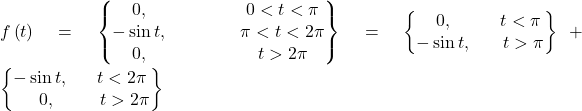
Solution

Using unit step function and the translated step function, the given piece-wise defined function can be written as,

$f\left(t\right)=\left[f_1\left(t\right)\left\{u\left(t\right)-u\left(t-\pi \right)\right\}+f_2\left(t\right).u\left(t-\pi \right)\right]+\left[f_2\left(t\right)\left\{-u\left(t-2\pi \right)-u\left(t-\pi \right)\right\}+f_3\left(t\right).u\left(t-2\pi \right)\right]$

$\begin{array}{l}f\left(t\right)=\left[0-\sin t.u\left(t-\pi \right)\right]+\left[\sin t.u\left(t-2\pi \right)+0\right]\\ \ \ \ \ \ \ \ =-\sin t.u\left(t-\pi \right)+\sin t.u\left(t-2\pi \right)\\ \ \ \ \ \ \ \ =\sin \left(t-\pi \right).u\left(t-\pi \right)+\sin \left(t-2\pi \right).u\left(t-2\pi \right)\end{array}$

Thus, the Laplace transform of this function is given as,

$\begin{array}{l}\mathcal{L}\left\{f\left(t\right)\right\}=\mathcal{L}\left\{\sin \left(t-\pi \right).u\left(t-\pi \right)\right\}+\mathcal{L}\left\{\sin \left(t-2\pi \right).u\left(t-2\pi \right)\right\}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =e^{-\pi s}L\left\{\sin t\right\}+e^{-2\pi }L\left\{\sin t\right\}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =e^{-\pi s}\frac{1}{s^2+1}+e^{-2\pi s}.\ \frac{1}{s^2+1}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{e^{-\pi s}+e^{-2\pi s}}{s^2+1}\end{array}$