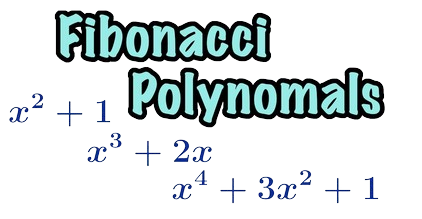Fibonacci Polynomials Method develop a new algorithm for solving linear and nonlinear integral equations using Galerkin weighted residual numerical method with Fibonacci polynomials [1]Fibonacci polynomials is given as

4.1.1 Methodology
Definition 4.1. Consider the integral equation of the 1st kind is given as
![]()
where u (t) is the unknown function, to be determined, , k (x,t), the kernel, is a continuous or discontinuous and square integrable function f(x), being the known function.
Now we use the technique of Galerkin method, [Lewis, 2], to find an approximate solution ū(x) of Eq. (4.9). For this, we assume that
![]()
where ![]() are Fibonacci polynomials of degree k defined in equation and
are Fibonacci polynomials of degree k defined in equation and ![]() are unknown parameters, to be determined. Substituting (4.10) into (4.9), we get
are unknown parameters, to be determined. Substituting (4.10) into (4.9), we get
![]() Then the Galerkin equations are obtained by multiplying both sides of Eq. (4.11) by
Then the Galerkin equations are obtained by multiplying both sides of Eq. (4.11) by ![]() and then integrating with respect to x from a to b , we have
and then integrating with respect to x from a to b , we have
![]()
Since in each equation, there are two integrals. The inner integrand of the left side is a function of x, and t , and is integrated with respect to t from a to x . As a result the outer integrand becomes a function of x only and integration with respect to x from a to b yields a constant. Thus for each j= 0,1,2,…,n we have a linear equation with n+1 unknowns ![]() and k= 0,1,2,…,n
and k= 0,1,2,…,n
Finally Eq. (4.12) represents the system of n+1 linear equations in n+1 unknowns, are given by
![]()

Now the unknown parameters are determined by solving the system of equations Eq. (4.13) and substituting these values of parameters in Eq. (4.10), we get the approximate solution ū(x) of the integral equation Eq. (4.9).
Definition 4.2. Consider the integral equation of the 2nd kind is
![]()
where u(t) is the unknown function, to be determined,k(x,t) , the kernel, is a continuous or discontinuous and square integrable function,f(x), u(x) and being the known function and λ is a constant. Proceeding as before
![]()
Where

Now the unknown parameters ![]() are determined by solving the system of equations Eq. (4.15) and substituting these values of parameters in Eq. (4.10), we get the approximate solution ū(x) of the integral equation Eq. (4.12).
are determined by solving the system of equations Eq. (4.15) and substituting these values of parameters in Eq. (4.10), we get the approximate solution ū(x) of the integral equation Eq. (4.12).
4.1.2 Applications of Fibonacci Polynomials Method
Example 4.3 Consider the Fredholm Integral equation [2]
![]() The exact solution of Eq. (4.16) is
The exact solution of Eq. (4.16) is
![]() Consider 3rd order Fibonicca Polynomials, i.e. for n=3 we have Eq. (4.16) is
Consider 3rd order Fibonicca Polynomials, i.e. for n=3 we have Eq. (4.16) is

Substituting Eq. (4.18) into Eq. (4.16)
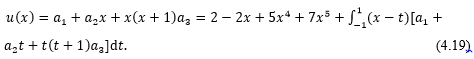 Now multiply Eq. (4.19) by
Now multiply Eq. (4.19) by ![]() and integrating both side from -1 to 1, we have
and integrating both side from -1 to 1, we have

the matrix form of Eq. (4.20) is
 After solving we get
After solving we get
![]()
Consequently we have the approximate solution is
![]()
TABLE 4.1 Comparison of the Exact Solution and Approximate Solutions of Eq. (4.16) for n=3 obtained from Fibonacci Polynomials Method


Fig 4.1 Comparison of Exact and Approximate Solutions of Eq. (4.16) for n=3.
Consider 5th order Fibonacci Polynomials, i.e. for we have Eq. (4.16) is
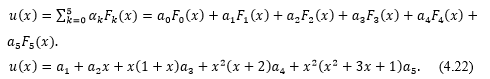 Substituting Eq. (4.22) into Eq. (4.16)
Substituting Eq. (4.22) into Eq. (4.16)
 Now multiply Eq. (4.23) by and integrating both side from -1 to 1, we have
Now multiply Eq. (4.23) by and integrating both side from -1 to 1, we have
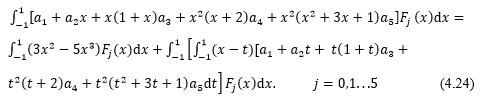
 after solving we get
after solving we get
![]()
Consequently we have approximate solution as
![]()
TABLE 4.2 Comparison of the Exact and Approximate Solutions of Eq. (4.16) for n=5 obtained from Fibonacci Polynomials Method
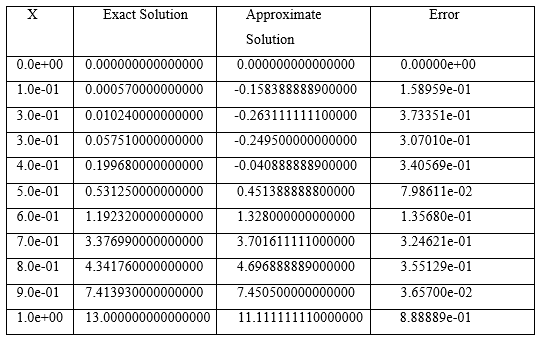

Fig 4.2 Comparison of Exact and Approximate Solutions of Eq. (4.16) for n= 5
Consider 6th order Fibonacci Polynomials, i.e. for n= 6 we have Eq. (4.16) is


Substituting Eq. (4.26) into Eq. (4.16)

Now multiply Eq. (4.27) by ![]() and integrating both side from -1 to 1, we have
and integrating both side from -1 to 1, we have

Now equation (4.28) can be written in the matrix form as,

After solving we get
![]() Consequently we have exact solution as
Consequently we have exact solution as
![]()
TABLE 4.3 Comparison of the Exact Solution and Approximate Solutions of Eq. (4.16) for n=6 obtained from Fibonacci Polynomials Method


Fig 4.3 Comparison of Exact and Approximate Solutions of Eq. (4.16) for n=6
Example 4.4 Consider the Volterra Integral equation [2]
![]() The exact solution of Eq. (4.30) is
The exact solution of Eq. (4.30) is
u (x) = 6(x)
According to the proposed technique, consider the trail solution
![]() Consider 1st order Fibonacci Polynomials, i.e. for n=1 we have Eq. (4.32) is
Consider 1st order Fibonacci Polynomials, i.e. for n=1 we have Eq. (4.32) is
 Substituting Eq. (4.32) into Eq. (4.29)
Substituting Eq. (4.32) into Eq. (4.29)
![]() Now multiply Eq. (27) by
Now multiply Eq. (27) by ![]() ,where j =0,1 and integrating both side from 0 to 1, we have
,where j =0,1 and integrating both side from 0 to 1, we have
![]()
now by solving Eq. (4.35) we get,
1.5000![]() =4.000
=4.000
after solving we get
![]() =1.800.
=1.800.
Consequently we have the approximate solution is
u(x) = 3.6667
Table 4.4 Comparison of the Exact Solution and Approximate Solutions of Eq. (4.40) for n=1, obtained from Fibonacci Polynomials Method


Fig 4.4 Comparison of Exact and Approximate Solutions of Eq. (4.40) for n=1.
Consider 2nd order Fibonacci Polynomials, i.e. for n=2, we have Eq. (4.42) is

Substituting Eq. (4.37) into Eq. (4.28)
![]()
Now multiply Eq. (3.45) by ![]() where j=0,1,2 and integrating both side from 0 to 1, we have
where j=0,1,2 and integrating both side from 0 to 1, we have
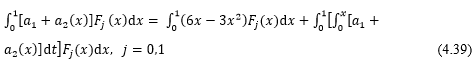
the matrix form of Eq. (4.39) is
![]()
After solving we get
![]()
Consequently we have the exact solution is
u(x)=6x (4.40)
Table 4.5 Comparison of the Exact Solution and Approximate Solutions of Eq. (4.40) for n=2 obtained from Fibonacci Polynomials Method


Fig 4.5 Comparison of Exact and Approximate Solutions of Eq. (4.40) for n=3.
Example 4.5 Consider the Abel’s Integral equation [2]
![]()
The exact solution of Eq. (4.41) is
u(x) = sin(x+3) ![]()
The transformation

According to the proposed technique, consider the trail solution
![]()
Consider 1st order Fibonacci Polynomials, i.e. for n=1 ,we have Eq. (4.44) is
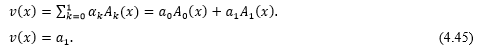
Substituting Eq. (4.45) into Eq. (4.41)
![]()
Now multiply Eq. (4.46) by ![]() where j=0,1 and integrating both side from 0 to 1,
where j=0,1 and integrating both side from 0 to 1,
we have
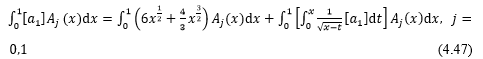
Eq. (4.47) can be written as,
![]() after solving we get
after solving we get ![]() consequently we have the approximate solution is
consequently we have the approximate solution is
![]()
now by putting back into Eq. (4.43) we get
![]()
Which is approximate solution.
TABLE 4.6 Comparison of the Exact Solution and Approximate Solutions of Eq. (4.41) for n=1, obtained from Fibonacci Polynomials Method

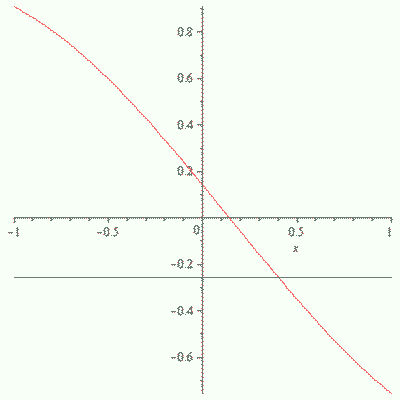
Fig 4.6 Comparison of Exact and Approximate Solutions of Eq. (4.41) for n=1.
Consider 2nd order Fibonacci Polynomials, i.e. for n=2, we have Eq. (4.44) is
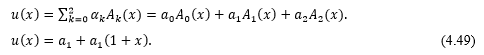
Substituting Eq. (4.49) into Eq. (4.44)
![]()
Now multiply Eq. (4.50) by ![]() where j=0,1 and integrating both side from 0 to 1, we have
where j=0,1 and integrating both side from 0 to 1, we have
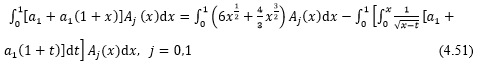
the matrix form of Eq. (4.51) is

after solving we get ![]() Consequently we have solution is
Consequently we have solution is
![]()
This gives exact solution by
![]()
obtained by using Eq. (4.43).
TABLE 4.7 Comparison of the Exact Solution and Approximate Solutions of Eq.(4.41) for n=3, obtained from Fibonacci Polynomials Method


Fig 4.7 Comparison of Exact and Approximate Solutions of Eq. (4.41) for n=3.
References
[1]. Benjamin, Arthur T.; Quinn, Jennifer J. “9.4 Fibonacci and Lucas Polynomial”.Proofs that Really Count. MAA. . ISBN 0-88385-333-7. (141)(2003).
[2]. A.M. Wazwaz, Linear and Nonlinear Integral Equations Method and Applications, Springer Heidelberg Dordrecht London, New York, 2011.
[3]. A.M. Wazwaz, Partial Differential Equations and Solitary Waves Theory, HEP and Springer, Beijing and Berlin, (2009).
[4]. J.Y. Xiao, L. H. Wen, D. Zhang, Solving second kind integral equations by periodic wavelet Galerkin method, Appl. Math. Comput. 175(2006), 508-518.