Dirac Delta Function

Dirac Delta Function , the unit step function (or the Heaviside function) helps us in solving differential equations with discontinuous forcing functions. However, there are many problems in Electrical/Mechanical/Mechatronics/Civil Engineering and Physics which involve impulsive force of every magnitude applied for just an instant. In such cases, an immense force acts over a very short time interval, resulting in sudden excitation to a system. For such like problems the unit step function is not really suitable.

Some examples of the above mentioned impulsive force are given as under:

a. The force exerted by the strike of a hammer.
b. A large force exerted by a heavy weight concentrated at a spot on a suspended beam, over a very small section of the beam.
c. The force exerted by a father’s slap to his son for some wrong doing which may put the latter on the right path for the rest of his life.
d. Point forces and couples employed in solid mechanics.
e. Impulsive forces applied in rigid body dynamics.
f. The force exerted by point masses in gravitational field theory.
g. The force exerted by point charges and multipoles in electrostatics.
h. The force exerted by point heat sources and pulses in the theory of heat conduction.
i. A brief application of a very large voltage in an electrical system.
j. The sudden discharge of energy contained in a capacitor.
k. The force exerted when a bat hits a ball.

Historical Background

In order to deal with the above mentioned types of violent forces of very short duration, mathematicians, physicists and engineers use the delta function, presumed to have been introduced by the Oxford University Nobel Laureate theoretical physicist Paul Adrian Maurice Dirac (1902-1984). Accordingly, it is called Dirac delta function, and sometimes impulse function.It has been revealed that during the nineteenth century ,both physicists and mathematicians use the delta function. The physicists viewed it as a pure mathematical idealization that did not exist in nature, while the mathematicians considered it as an intuitive physical notion without any mathematical reality (J. Lützen: The Prehistory of the Theory of Distribution, Springer Verlag pp-232(1982).
Although the Dirac delta function was in use earlier, however, the scientists and engineers were actually attracted by this function after the work of Oliver Heaviside (1850-1925) and the birth of Electrical Engineering. While dealing with a cable which is grounded on both sides, Heaviside introduced the delta function via its sifting property (see below). Accordingly, like the Laplace transforms, the delta function also became a fundamental tool for the electrical engineers.

The Dirac delta function was defines as,

$\delta \left(t\right)=\left\{\begin{matrix}\infty ,&\ \ \ \ \ \ \ t=0\\0,&\ \ \ \ \ \ \ t\ \ne 0\end{matrix}\right\}$ (10.1)

such that

$\int _{-\infty }^{\infty }\delta \left(t\right)\ dt=1$ (10.2)

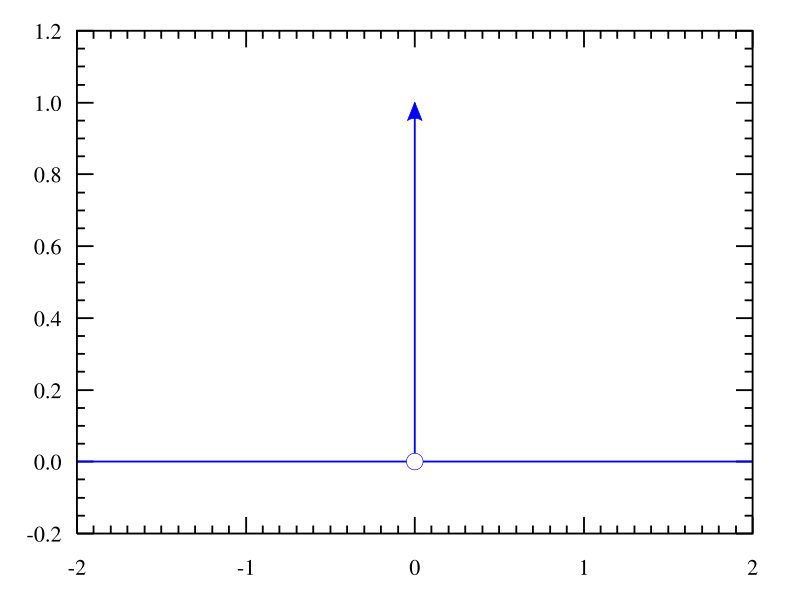
With the exception of t=0, where its value is endlessly huge to the point where its total integral equals 1, this “function” has a value of zero everywhere.Geometrically it is shown in Fig.10.1.

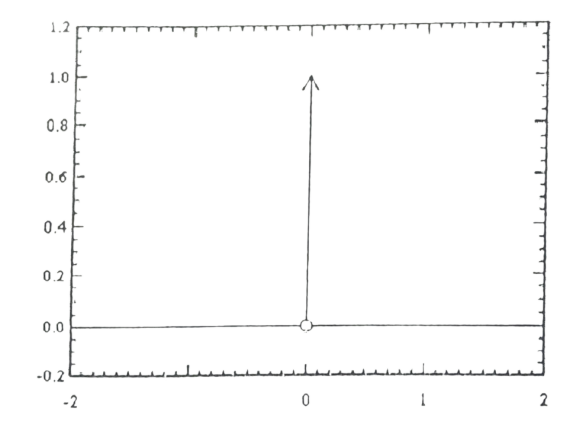
Fig. 10.1 The Dirac Delta Function

However, no conventional function could be found that would satisfy both of the above
mentioned equations. Therefore, although this peculiar natured function was being used as a fundamental tool by the electrical engineers by 1945, yet there were several schools
of thought concerning its exact nature.
Many physicists considered the delta function as the limit of the sequence of strongly
peaked functions $\delta _n\left(t\right)$ as,

$\delta _n\left(t\right)=\lim _{n\to +\infty }\delta _n\left(t\right),$ (10.3)

where, the candidates for $\delta _n\left(t\right)$ included,

$\delta _n\left(t\right)=\frac{n}{\pi }\ \frac{1}{1+n^2t^2} (10.4)$

$\delta _n\left(t\right)=\frac{n}{\sqrt{\pi }}\ e^{-n^2t^2}(10.5)$

$\delta _n\left(t\right)=\frac{1}{n\pi }\ \frac{\sin ^2\left(nt\right)}{t^2}(10.6)$

Because it matched their physical intuition of a point mass or a point charge, this method was well-liked by physicists. However, the drawback of this approach was that the limits of the above sequences may not exist.The electrical engineers viewed the delta function from another angle which involved the unit step function,

$u\left(t\right)=\left\{\begin{matrix}0,&t<0\\ 1,\ \ \ \ \ \ \ \ \ &t>0\end{matrix}\right\}$ (10.7)

Accordingly, the delta function was merely the derivative of the unit step function as,
$\delta \left(t\right)=\frac{d}{dt}u\left(t\right)=u^{^{\prime }}\left(t\right)$ (10.8)

The difficulty with this approach was that the derivative does not exist at $t=0$ .
Certain other scientists and engineers defined the delta function based on its filtering, (or sifting) property as,

$\int _{-\infty }^{\infty }f\left(t\right)\delta \left(t-a\right)dt=f\left(a\right)$ (10.9)

It is called the filtering (or sifting) property of the delta function since $\delta \left(t-a\right)$ acts on f(t) as a sieve, and sifts out or selects from all possible values of f(t), its value f(a) at the point t=a only. The difficulty with this approach is that there is no such conventional function as $\delta \left(t-a\right)$ with the above mentioned property. We shall discuss the above mentioned characteristics of the Dirac delta function in detail in what follows.

Unit Impulse

Consider a large force f(t) that acts for a very short time interval $a-\epsilon \le t\le a+\epsilon$ , with f(t)=0 outside the interval. In such a case, the total effect of this sudden excitation administered to the system is given as,

$I=\int _{-\infty }^{\infty }f\left(t\right)dt=\int _{a-\epsilon }^{a+\epsilon }f\left(t\right)dt,\ \ \ \ \epsilon >0$ (10.10)

The value of this integral is a measure of the strength of the sudden excitation, and is called the impulse of the force f(t) over the interval $\left[a-\epsilon ,\ a+\epsilon \right]$ , with units of force times time $[MLT^{-1}]$ . In order to study the effect of such a force we would try to construct a mathematical model in which the unknown force f(t) is replaced with a simple and explicit force that has the same impulse as that of the force f(t) and does not depend on as to how f(t) varies with time t. We choose this force in such a way that the total impulse is unity. Accordingly we write the function,

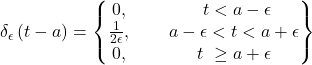$\delta _{\epsilon }\left(t-a\right)=\left\{\begin{matrix}0,&\ \ \ \ \ t<a-\epsilon \\ \frac{1}{2\epsilon },&\ \ \ \ a-\epsilon <t<a+\epsilon \\ 0,&\ \ \ \ t\ \ge a+\epsilon \end{matrix}\right\}$ (10.11)

where $<em>a</em> > 0, \epsilon > 0$ (see Fig. 10.2). This function could serve as a mathematical model for the above mentioned sudden violent force f(t). When $\epsilon$ is small, the function $\delta _{\epsilon }\left(t-a\right)$ is essentially constant, having a large value, which is “ON” for a very brief interval of time around t=a. Accordingly Eqn.(10.10) becomes:

$I=\int _{-\infty }^{\infty }f\left(t\right)dt=\int _{a-\epsilon }^{a+\epsilon }\delta _{\epsilon }\left(t-a\right)dt,\ \ \ \ \ \ \epsilon >0$ (10.12)

Fig.10.2

Fig.10.3

The behaviour of the function $\delta _{\epsilon }\left(t-a\right), as \epsilon →0$ is shown in Fig. 10.3. Here, the function $\delta _{\epsilon }\left(t-a\right)$ is made to act over shorter and shorter interval by allowing $\epsilon$ tend to zero. Accordingly, although the interval about t = a is shrinking to zero, yet we want the value of the above integral, I, to be equal to unity, i.e.,

$\ \ \lim _{\epsilon \to 0}I=\lim _{\epsilon \to 0}\int _{-\infty }^{\infty }f\left(t\right)dt=\lim _{\epsilon \to 0}\int _{a-\epsilon }^{a+\epsilon }\delta _{\epsilon }\left(t-a\right)dt,\ \ \ \ \ \ \epsilon >0$
$=\lim _{\epsilon \to 0}\int _{-\infty }^{\infty }\frac{1}{2\epsilon }dt=\frac{1}{2\epsilon }\left[\left(a+\epsilon \right)-\left(a-\epsilon \right)\right]=1$ (10.13)

Thus $\delta _{\epsilon }\left(t-a\right)$ has a unit impulse for any non-zero value of $\epsilon$ . Because of this inherent property the function $\delta _{\epsilon }\left(t-a\right)$ , it is also called a unit impulse. This, in fact, amounts to
normalizing the impulse.

Dirac Delta Function

Eqn.(10.13) illustrates that the precise time interval during which the force acts is un-important. Therefore, it is tempting to think of an instantaneous impulse that occurs at the instant t = a. Accordingly, in practical problems it is convenient to replace the above mentioned unit impulse “function” $\delta _{\epsilon }\left(t-a\right)$ , by another unit impulse “function” which approximates the latter as under:

$\delta \left(t-a\right)=\lim _{\epsilon \to 0}\delta _{\epsilon }\left(t-a\right)$ (10.14)

and satisfies the two (inconsistent) mathematical properties:

$\delta \left(t-a\right)=\left\{\begin{matrix}\infty ,&\ \ \ \ \ t=a\\ 0,&\ \ \ \ \ t\ \ne a\end{matrix}\right\}$ (10.15)

and

$\ \int _{-\infty }^{\infty }\delta \left(t-a\right)dt=\int _{a-\epsilon }^{a+\epsilon }\delta \left(t-a\right)dt=1$ (10.16)

$\delta \left(t-a\right)$ is called the Dirac delta function, and in the context of signal processing it is called the unit impulse function, which imparts an impulse of magnitude “one” at an arbitrary point t = a, but is zero for all other values of t. The impulsive forcing functions can conveniently be represented by means of the Dirac delta function.
As mentioned above (see Eqns.(10.1), and (10.2)), the Dirac delta “function” is also denoted by $\delta \left(t\right)$ , which corresponds to unit impulse at t = 0, and has the properties,

$\delta \left(t\right)=\left\{\begin{matrix}\infty ,&\ \ \ \ \ t=0\\ 0,&\ \ \ \ \ t\ \ne 0\end{matrix}\right\}$

and

$\int _{-\infty }^{\infty }\delta \left(t\right)dt=\int _{-\epsilon }^{\epsilon }\ \delta \left(t\right)dt=1$

It should be noted that, strictly speaking, no function—at least not a typical one covered in elementary calculus—satisfies both of the aforementioned two equations, 10.15 and 10.16. However, for many purposes it can be manipulated as such. The “function” $\delta$ defined by these equations is an example of a generalized function. These functions are also called distributions, whose theory was developed in 1936 by the Russsian mathematician Sergi L’Vovich Sobolev (1908-1989).In 1945 this theory was discussed under wider aspects by the French mathematician Laurent Schwartz (1915-2002). After publication of the theory of distributions by Schwartz, the concept of generalized functions has had tremendous impact on many areas of mathematics, particularly partial differential equations.