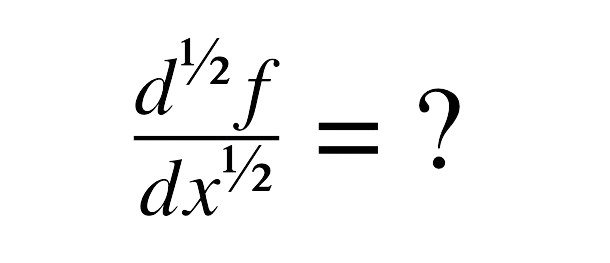
Bell Polynomials Method

Bell Polynomials Method ,we develop a new algorithm for solving linear and nonlinear integral equations using Galerkin weighted residual numerical method with Bell polynomials [1]. Bell polynomials is given as

$B_m(x)=(x(BI_n+d/dxBI_n)$ (3.259)

$B_0=1,$

$\begin{array}{l}B_1=x,\end{array}$
$\begin{array}B_2=x(x+1),\end{array}$

$B_3=〖x(x^2+3x+1),$

$B_4=x(x^3+6x^2+7x+1),$

3.9.1 Methodology

Definition 3.9. Consider the integral equation of the 1^st kind is given as

$f(x)=λ\int _{\alpha \left(x\right)}^{\beta \left(x\right)}K(x,t)\ u(t)\ dt,a\le x\le b,$ (3.260)

where u(t) is the unknown function, to be determined,k(x,t) , the kernel, is a continuous or discontinuous and square integrable function,f(x) being the known function.

Now we use the technique of Galerkin method, [Lewis, 2], to find an approximate solution of Eq. (3.260). For this, we assume that

$ũ(x)=\sum _{k=0}^n〖a_kB_k(x),$ (3.261)

where $B_k\left(x\right)$ are Bell polynomials of degree $k$ defined in equation (3.259) and latex]a_k[/latex] are unknown parameters, to be determined. Substituting (3.261) into (3.260), we get

$f(x)=λ\sum _{k=0}^na_k\int _a^x〖K(x,t)B_k(t)dt.$ (3.262)

Then the Galerkin equations are obtained by multiplying both sides of (3.262) by $\begin{array}{l}A_j\left(x\right)\end{array}$ and then integrating with respect to x from a to b , we have

$B_j(x)dx=λ\sum _{k=0}^na_k\int _a^b(\int _a^xK(x,t)B_k(t)dt〗)B_j(x)dx,〗j=0,1,2,...,n.$ (3.263)

Since in each equation, there are two integrals. The inner integrand of the left sides is a function of x, and t, and is integrated with respect to t from a to x . As a result the outer integrand becomes a function of x only and integration with respect to x from a to b yields a constant. Thus for each j=0,1,2,…,n we have a linear equation with n+1 unknowns $a_k$ ,k=0,1,2,…,n.

Finally (3.263) represents the system of n+1 linear equations in n+1 unknowns, are given by

$λ\sum _{k=0}^n〖a_kK_{k,j}=F_j;k,j=0,1,2,\dots n〗$ (3.264)

where

$\begin{array}{l}K_{k,j}=\int _a^b〖(\int _a^x〖K(x,t)B_k(t)dt〗)B_j(x)dx,〗k,j=0,1,2,\dots n, F_j=\int _a^bf(x)B_j(x)dx,j=0,1,2,\dots n.\end{array}$

Now the unknown parameters $a_k$ are determined by solving the system of equations (3.264) and substituting these values of parameters in (3.260), we get the approximate solution of the integral equation (3.260).

Definition 3.10. Consider the integral equation of the 2^nd kind is

$f(x)=c(x)u(x)+λ\int _{α\left(x\right)}^{^{β\left(x\right)}}K(x,t)u(t)dt,a\le x\le b.$ (3.265)

where u(t) is the unknown function, to be determined,k(x,t) , the kernel, is a continuous or discontinuous and square integrable function, f(x) and u(x) being the known function and λ is a constant. Proceeding as before

$\sum _{k=0}^n〖a_kK_{k,j}=F_j; k,j=0,1,2,\dots n〗$ (3.266)

where

$K_{k,j}=\int _a^b〖(c(x)B_k(x)+λ\int _a^x〖K(x,t)B_k(t)dt〗)B_j(x)dx,〗k,j=0,1,2,\dots n,$

and

$F_j=\int _a^bf(x)B_j(x)dx,j=0,1,2,\dots n.$

Now the unknown parameters $a_k$ are determined by solving the system of equations (3.266) and substituting these values of parameters in (3.261), we get the approximate solution of the integral equation (3.265).

3.9.2 Applications of Bell Polynomials Method

Example 3.40 Consider the Volterra Integral equation [2]

$u(x)=1-\int _0^x〖(x-t)〗u(t)dt.$ (3.267)

The exact solution of Eq. (3.267) is

$u(x)=\cos x.$ (3.268)

According to the proposed technique, consider the trail solution

$u(x)=\sum _{k=0}^n〖a_kB_k(x).〗$ (3.269)

Consider 5^th order Bell’s polynomials, i.e. for n=5 we have Eq. (3.269) is

$u(x)=\sum _{k=0}^5〖a_kB_k(x)=a_0B_0(x)+a_1B_1(x)+a_2B_2(x)+a_3B_3(x)++a_4B_4(x)+a_5B_5(x).$

$u(x)=a_0+a_1(x)+a_2(x^2+x)+a_3(x^3+3x^2+x)+a_4(x^4+6x^3+7x^2+x)+a_5(x^5+10x^4+25x^3+15x^2+x).$ (3.270)

Substituting Eq. (3.270) into Eq. (3.267)

$a_0+a_1(x)+a_2(x^2+x)++a_3(x^3+3x^2+x)+a_4(x^4+6x^3+7x^2+x)+〖a〗_5(x^5+10x^4+25x^3+15x^2+x)=1-\int _0^x〖(x-t)〗[a_0+a_1(x)+〖a〗_2(x^2+x)+a_3(x^3+3x^2+x)+a_4(x^4+6x^3+7x^2+x)+a_5(x^5+10x^4+25x^3+15x^2+x)]dt.$ (3.271)

Now multiply Eq. (3.271) by $B_j\left(x\right)$ , j=0,1…,5 and integrating both sides from 0 to 1, we have

$\int _0^1〖[a_0+a_1(x)+a_2(x^2+x)++a_3(x^3+3x^2+x)+a_4(x^4+6x^3+7x^2+x)+a_5(x^5+10x^4+25x^3+15x^2+x)]B_j〗(x)dx=\int _0^1〖B_j(x)〗dx-\int _0^1〖[\int _0^x(x-t)[a_0+a_1(t)+a_2(t^2+t)++a_3(t^3+3t^2+t)+a_4(t^4+6t^3+7t^2+t)+a_5(t^5+10t^4+25t^3+15t^2+t)]dt]B_j(x)dx,〗j=0,1,\dots 5.$ (3.272)

The matrix form of Eq. (3.272) is

$\left[\begin{matrix}1.166666667&\dots &14.46726191\\ \vdots &\vdots &\vdots \\ 18.40178572&\dots &427.4156363\end{matrix}\right]\left[\begin{matrix}a_0\\ a_1\\ \vdots \\ a_5\end{matrix}\right]=\left[\begin{matrix}1.000000000\\ 0.500000000\\ \vdots \\ 13.91666667\end{matrix}\right]$

After solving we get,

$a_0$ =0.9999572449 , $a_1$ = 0.5993116899 , $a_2$ = 0.006727811425.

Consequently we have the approximate solution is

$u(x)=0.9999572449+0.001249710615x+⋯+0.006727811425x^5$

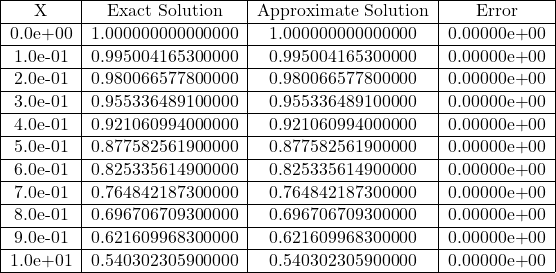
Table 3.37 Comparison of the Exact Solution and Approximate Solutions of Eq. (3.267) for n=5 obtained using Bell Polynomials Method

$\begin{tabular}{|c|c|c|c|} \hline X & Exact Solution & Approximate Solution & Error \\ \hline 0.0e+00 & 1.000000000000000 & 1.000001332000000 & 1.33165e-06 \\ \hline 1.0e-01 & 0.995004165300000 & 0.995003647100000 & 5.18200e-07 \\ \hline 2.0e-01 & 0.980066577800000 & 0.980066812800000 & 2.35000e-07 \\ \hline 3.0e-01 & 0.955336489100000 & 0.955336872600000 & 3.83500e-07 \\ \hline 4.0e-01& 0.921060994000000 & 0.921060880400000 & 1.13600e-07 \\ \hline 5.0e-01 & 0.877582561900000 & 0.877582152200000 & 4.09700e-07 \\ \hline 6.0e-01 & 0.825335614900000 & 0.825335517500000 & 9.74000e-08 \\ \hline 7.0e-01 & 0.764842187300000 & 0.764842571600000 & 3.84300e-07 \\ \hline 8.0e-01 & 0.696706709300000 & 0.696706926600000 & 2.17300e-07 \\ \hline 9.0e-01 & 0.621609968300000 & 0.621609463200000 & 5.05100e-07 \\ \hline 1.0e+01 & 0.540302305900000 & 0.540303583000000 & 1.27710e-06 \\ \hline \end{tabular}$

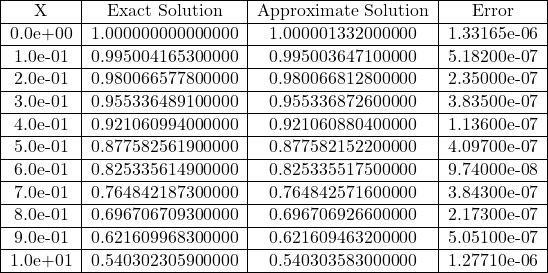
Fig 3.37 Comparison of Exact and Approximate Solutions of Eq. (3.267) for n=5.

Now consider 25^th order Bell Polynomials, i.e. for we have Eq. (3.269) is

$u(x)=\sum _{k=0}^{25}〖a_kB_k(x)〗=a_0B_0(x)+a_1B_1(x)+a_2B_2(x)\dots .+a_{25}B_{25}(x).$

$u(x)=a_0+a_1(x)+a_2(x^2+x)+⋯+a_{25}(x+141197991025x^2+\dots 300x^{23}+x^{24}).$ (3.273)

Substituting Eq. (3.273) into Eq. (3.267)

$a_0+a_1(x)+a_2(x^2+x)+⋯+a_{25}(x+141197991025x^2+⋯300x^{23}+〖x〗^{24})=1-\int _0^x〖(x-t)〗[a_0+a_1(t)+a_2(t^2+t)+⋯+a_{25}(t+141197991025t^2+⋯+300t^{23}+t^{24})]dt.$ (3.274)

Now multiply Eq. (3.274) by $B_j\left(x\right)$ , j=0,1,2,…,25 and integrating both sides from 0 to 1, we have

$\int _0^1〖[a_0+a_1(x)+a_2(x^2+x)+⋯+a_{25}(x+141197991025x^2+⋯300x^{23}+〖x〗^{24})]〗B_j(x)dx=\int _0^1〖B_j(x)〗dx-\int _0^1〖[\int _0^x(x-t)[a_0+a_1(t)+a_2(t^2+t)+⋯+〖a〗_{25}(t+141197991025t^2+⋯300t^{23}+t^{24}))]dt]B_j(x)dx,$ j=0,1,2,…,25 (3.275)

The matrix form of Eq. (3.275) is

$\left[\begin{matrix}1.166666667&\dots &4.452081399〖10〗^{17}\\ \vdots &\ \vdots &\ \ \ \ \ \ \ \ \ \ \ \vdots \\ 6.271098472〖10〗^{17}&\dots &1.074254826〖10〗^{36}\end{matrix}\right]\left[\begin{matrix}a_0\\ a_1\\ \ \vdots \\ a_{25}\end{matrix}\right]=\left[\begin{matrix}1.00000000000\\ 0.50000000000\\ \ \ \ \ \ \ \ \ \vdots \\ 4.419861486〖10〗^{17}\end{matrix}\right]$

After solving we get,

$〖a〗_0=0.9999942998,〖a〗_1=0.4862702700,\dots ..a_{24}=1.200016426〖10〗^{\left((-18\right)},a_{25}=-1.054550673〖10〗^{\left((-19\right)}.$

Consequently we have the approximate solution is

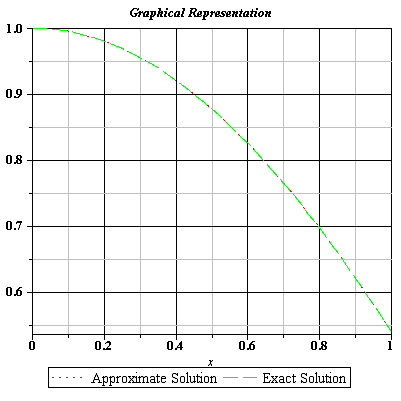
$u(x)=-1.268283640〖10〗^{\left((-18\right)}x^{19}-0.001937194290x^{13}+⋯-0.5020785808x^2+0.0002406743187x.$

Fig 3.38 Comparison of Exact and Approximate Solutions of Eq. (3.267) for n=25.

Table 3.38 Comparison of the Exact Solution and Approximate Solutions of Eq. (3.267) for obtained using Bell Polynomials Method

$\begin{tabular}{|c|c|c|c|} \hline X & Exact Solution & Approximate Solution & Error \\ \hline 0.0e+00 & 1.000000000000000 & 1.000000000000000 & 0.00000e+00 \\ \hline 1.0e-01 & 0.995004165300000 & 0.995004165300000 & 0.00000e+00 \\ \hline 2.0e-01 & 0.980066577800000 &0.980066577800000 & 0.00000e+00 \\ \hline 3.0e-01 & 0.955336489100000 & 0.955336489100000 & 0.00000e+00 \\ \hline 4.0e-01& 0.921060994000000 &0.921060994000000 & 0.00000e+00 \\ \hline 5.0e-01 & 0.877582561900000 & 0.877582561900000 & 0.00000e+00 \\ \hline 6.0e-01 & 0.825335614900000 & 0.825335614900000 & 0.00000e+00 \\ \hline 7.0e-01 & 0.764842187300000 & 0.764842187300000 & 0.00000e+00 \\ \hline 8.0e-01 & 0.696706709300000 & 0.696706709300000 & 0.00000e+00 \\ \hline 9.0e-01 & 0.621609968300000 & 0.621609968300000 & 0.00000e+00 \\ \hline 1.0e+01 & 0.540302305900000 & 0.540302305900000 & 0.00000e+00 \\ \hline \end{tabular}$

Now consider 50^th order Bell Polynomials, i.e. for n=50, we have Eq. (3.269) is

$u(x)=\sum _{k=0}^{50}〖a_kB_k(x)〗=a_0B_0(x)+a_1B_1(x)+a_2B_2(x)\dots .+a_{50}B_{50}(x).$

$\left(u(x)=a_0+a_1(x)+a_2(x^2+x)+⋯+a_{50}(x+⋯+710500x^{47}+1225x^{48}+x^{49}\right).$ (3.276)

Substituting Eq. (3.276) into Eq. (3.267)

$a_0+a_1(x)+a_2(x^2+x)+⋯+a_{50}(x+⋯+710500x^{47}+1225x^{48}+x^{49})=1-\int _0^x(x-t)[a_0+a_1(t)+a_2(t^2+t)+⋯+a_{50}(t+⋯+710500t^{47}+1225t^{48}+t^{49})]dt.$ (3.277)

Now multiply Eq. (3.277) by $B_j\left(x\right)$ ,j=0,1,2,…,50 and integrating both sides from 0 to 1, we have

$\int _0^1〖[a_0+a_1(1+x)+a_2(1+x^2+2x)+⋯+a_{50}(x+⋯+710500x^{47}+1225x^{48}+〖x〗^{49})]A_j(x)dx\int _0^1A_j(x)〗dx-\int _0^1〖[\int _0^x(x-t)[a_0+a_1(t)+〖a〗_2(t^2+t)+⋯+a_{50}(t+⋯+710500t^{47}+1225t^{48}+〖t〗^{49}))]dt]A_j(x)dx,〗j=0,1,\dots ,50.$ (3.278)

The matrix form of Eq. (3.278) is

$\left[\begin{matrix}1.16666666667&\dots &1.072211729〖10〗^{46}\\ \ \ \ \ \ \ \ \ \ \ \vdots &\ \vdots &\ \ \ \ \ \ \ \ \ \ \vdots \\ 1.547960211〖10〗^{46}&\dots &1.019358344〖10〗^{93}\end{matrix}\right]\left[\begin{matrix}a_0\\ a_1\\ \ \vdots \\ a_{50}\end{matrix}\right]=\left[\begin{matrix}1.000000000000\\ 0.500000000000\\ \ \ \ \ \ \ \ \ \ \ \ \vdots \\ 1.069115893〖10〗^{46}\end{matrix}\right]$

After solving we get,

$a_0=0.999999996132,a_1=0.5404170645,\dots ,a_{49}=9.424749020〖10〗^{\left((-47\right)},a_{50}=-1.887026〖109910〗^{\left((-47\right)}.$

Consequently we have the approximate solution is

$u(x)=0.04379085549x^{15}-3.429158733+0.3278120226x^6-0.3015238605x^7.$

Table 3.39 Comparison of the Exact Solution and Approximate Solutions of Eq. (3.267) for obtained using Bell

Polynomials Method

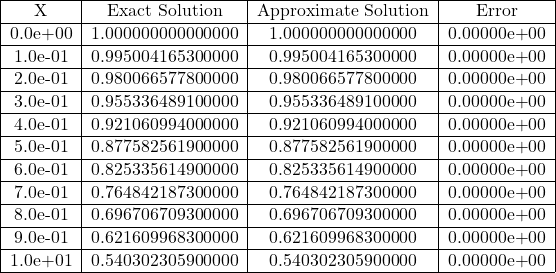
Fig 3.39 Comparison of Exact and Approximate Solutions of Eq. (3.267) for n=50.

Example 3.41 Consider the weakly singular Volterra Integral equation [2]

$u(x)=x^2-128/45x^{\frac{9}{4}}+\int _0^x1/(x-t)^{\frac{3}{4}}u(t)dt.$ (3.279)

The exact solution of Eq. (3.279) is

$u(x)=x^2$ (3.280)

According to the proposed technique, consider the trail solution

$u(x)=\sum _{k=0}^na_kB_k(x).$ (3.281)

Consider 1^st order Bell Polynomials, i.e. for n=1 we have Eq. (3.281) is

$u(x)=\sum _{k=0}^1a_kB_k(x)=a_0B_0(x)+a_1B_1(x).$

$u(x)=a_0+a_1(1+x).$ (3.282)

Substituting Eq. (3.282) into Eq. (3.279)

$a_0+a_1(x)=x^2-128/45x^{\frac{9}{4}}+\int _0^x1/(x-t)^{\frac{3}{4}}[a_0+a_1(t)]dt.$ (3.283)

Now multiply Eq. (3.283) by $B_j\left(x\right)$ ,j=0,1 and integrating both sides from 0 to 1, we have

$\int _0^1[a_0+a_1(x)]B_j(x)dx=\int _0^1(x^2-128/45x^{\frac{9}{4}})B_j(x)dx+\int _0^1[\int _0^x1/(x-t)^{\frac{3}{4}}[a_1+a_2(t)]dt]A_j(x)dx,j=0,1.$ (3.284)

The matrix form of Eq. (3.284) is

$\left[\begin{matrix}-11/5&-83/90\\ -23/18&-127/195\end{matrix}\right]\left[\begin{matrix}a_0\\ a_1\end{matrix}\right]=\left[\begin{matrix}317/585\\ 1283/3060\end{matrix}\right]$

After solving we get,

$a_0=-1570969/11841622\ ,\ a_1=411751/455447.$

Consequently we have the approximate solution is

$u(x)=-1570969/11841622+411751/455447x.$

Table 3.40 Comparison of the Exact Solution and Approximate Solutions of Eq. (3.279) for obtained using Bell Polynomials Method

$\begin{tabular}{|c|c|c|c|} \hline X & Exact Solution & Approximate Solution & Error \\ \hline 0.0e+00 & 0.000000000000000 & -0.132665018400000 & 1.32665e-01 \\ \hline 1.0e-01 & 0.010000000000000 & -0.042259109480000 & 5.22591e-02 \\ \hline 2.0e-01 & 0.040000000000000 & 0.048146799400000 & 8.14680e-03 \\ \hline 3.0e-01 & 0.090000000000000 & 0.138552708400000 & 4.85527e-02 \\ \hline 4.0e-01& 00.160000000000000 & 0.228958617300000 & 6.89586e-02 \\ \hline 5.0e-01 & 0.250000000000000 & 0.319364526200000 & 6.93645e-02 \\ \hline 6.0e-01 &0.360000000000000 & 0.409770435100000 & 4.97704e-02 \\ \hline 7.0e-01 & 0.490000000000000 & 0.500176344000000 & 1.01763e-02 \\ \hline 8.0e-01 & 0.640000000000000 & 0.590582253000000 & 4.94177e-02 \\ \hline 9.0e-01 & 0.810000000000000 & 0.680988161900000 & 1.29012e-01 \\ \hline 1.0e+01 & 1.000000000000000 & 0.771394070800000 & 2.28606e-01 \\ \hline \end{tabular}$

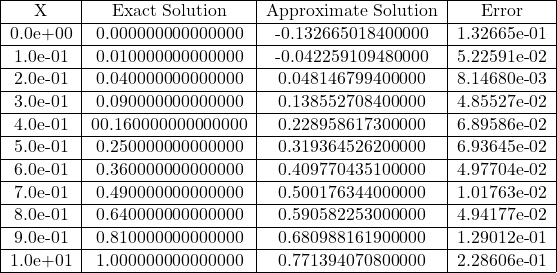
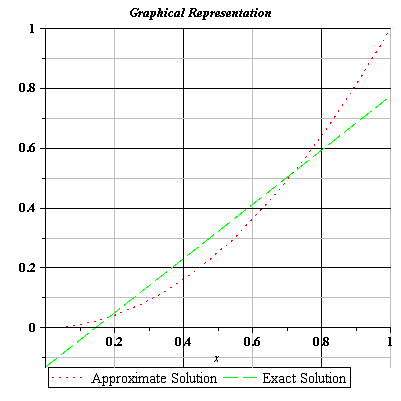
Fig 3.40 Comparison of Exact and Approximate Solutions of Eq. (3.279) for n=1.

References

[1]. Zhu, S, The generalized Riccati equation mapping method in non-linear evolution equation: Application to (2+1)-dimensional Boiti-Leon- Pempinelle equation.

[2]. A.M. Wazwaz, Linear and Nonlinear Integral Equations Method and Applications, Springer Heidelberg Dordrecht London, New York, 2011.

References