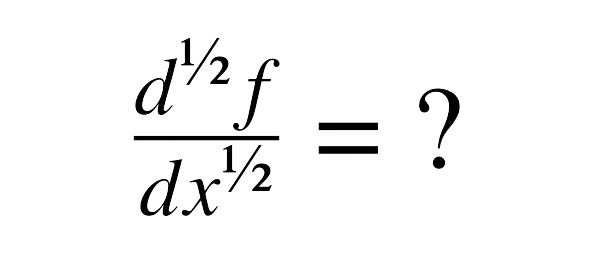
Applications of Gegenbauer Polynomials Method

Applications of Gegenbauer Polynomials Method,we develop a new algorithm for solving linear and nonlinear integral equations using Galerkin weighted residual numerical method with Gegenbauer polynomials. Gegenbauer polynomials [1] is given as

$G_m(x)=\left(\frac{1}{n}(2x(n+α-1)\right)GI_{n-1}-(n+2α-2)GI_{n-2}.$ (3.96)

$G_0=1,$

$G_1=x-\frac{1}{2},$ ,

$G_2=x^2-\frac{4}{3}x+\frac{2}{3},$

$G_3=x^3-\frac{11}{4}x^2+\frac{11}{3}x-\frac{11}{6},$

$G_4=x^4-\frac{26}{5}x^3+\frac{143}{10}x^2-\frac{286}{15}x+\frac{143}{15},$

Applications of Gegenbauer Polynomials Method

3.8.1 Volterra Integral Equation

Consider the Volterra Integral equation [2] as

$u(x)=5+2x^2-\int _0^x(x-t)\ u(t)dt.$ (3.104)

The exact solution of Eq. (3.104) is

$u(x)=4+\cos x.$ (3.105)

According to the proposed technique, consider the trail solution

$u(x)=\sum _{k=0}^na_kG_k(x)$ (3.106)

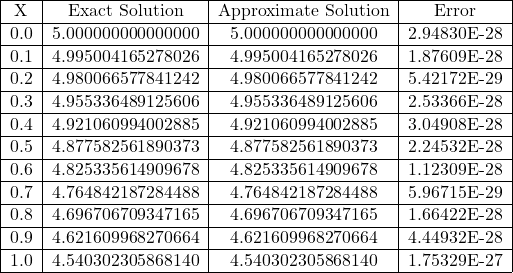
Consider 20^th order Gegenbauer Polynomials, i.e. for n=20, we have Eq. (3.106) is

$u(x)=\sum _{k=0}^{20}a_kG_k(x)=a_0G_0(x)+a_1G_1(x)+⋯+a_{20}G_{20}(x).$

$u(x)=a_0+2βxa_1+(2x^2β+2x^2β^2-β)a_2+\ ^{....}\frac{1}{110}β-20x^2β+\dots β^{19})a_{20}.$ (3.107)

Substituting Eq. (3.107) into Eq. (3.104)

$u(x)=a_0+2βxa_1+(2x^2β+2x^2β^2-β)a_2+⋯\left(\left(\frac{1}{10}β-20x^2β+\dots β^{19}\right)a_{20}=5+2x^2-\int _0^x(x-t)u(t)dt.\right)$ (3.108)

Now multiply Eq. (3.108) by $G_j(x),\ j=0,1,\dots ,20$ and integrating both sides from 0 to 1, we have

$\int _0^1((a_0+2βxa_1+(2x^2β+2x^2β^2-β)a_2+⋯\left(\left(\frac{1}{10}β-20x^2β+⋯β^{19}\right)a_{20}\right)G_j(x)dx=\int _0^1(5+2x^2)G_j(x)dx+\int _0^1[\int _0^x[a_0+2βta_1+(2t^2β+2t^2β^2-β)a_2+⋯\frac{1}{10}β-20t^2β+\dots β^{19})a_{20}]dt]G_j(x)dx,\ j=0,1,\dots ,20.$ (3.109)

Now for $\beta =1$ the matrix form of Eq. (3.109) is

$\left[\begin{matrix}2.3333&\ \ \ 0&0.4667\ \ \ ...\ \ \ \ \ \ 0.0997\\ 0&2.9333&\ \ \ 0\ \ \ \ \ \ \ \ \ ...\ \ \ \ \ \ \ \ \ 0\\ \vdots &\ \ \ \vdots &\ \ \ \vdots \ \ \ \ \ \ \ \ \ \ ...\ \ \ \ \ \ \ \ \vdots \ \\ 0.1430&\ \ \ 0&0.2717\ \ \ ...\ \ \ \ 5.0061\end{matrix}\right]\left[\begin{matrix}a_0\\ a_1\\ \ \ \vdots \\ a_{20}\end{matrix}\right]=\left[\begin{matrix}11.333\\ \ \ \ 0\\ \ \ \ \vdots \\ 0.6676\end{matrix}\right]$

After solving we get,

$a_0=4.88102,\ a_2=7.25025,\dots ,\ a_{20}=3.8746\times 10^{-25}.$

Consequently we have the approximate solution is,

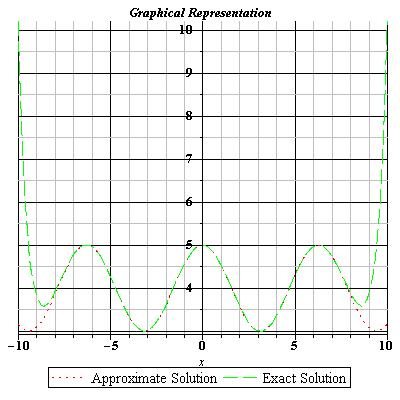
$u(x)=4.9999-1.1288\times 10^{-50}x+⋯+4.0628\times 10^{-19}x^{20}.$

Fig 3.10 Comparison of Exact and Approximate Solutions of Eq. (3.104) for n=20.

Table 3.10 Comparison of Exact and Approximate Solutions of Eq. (3.104) for n=20 obtained from Gegenbauer polynomials Method

$\begin{tabular}{|c|c|c|c|} \hline X & Exact Solution & Approximate Solution & Error \\ \hline 0.0 & 5.000000000000000 & 5.000000000000000 & 2.94830E-28\\ \hline 0.1 & 4.995004165278026 & 4.995004165278026 &1.87609E-28 \\ \hline 0.2 & 4.980066577841242 & 4.980066577841242 & 5.42172E-29 \\ \hline 0.3 & 4.955336489125606 & 4.955336489125606 & 2.53366E-28 \\ \hline 0.4 & 4.921060994002885 & 4.921060994002885 & 3.04908E-28 \\ \hline 0.5 & 4.877582561890373 & 4.877582561890373 & 2.24532E-28 \\ \hline 0.6 & 4.825335614909678 & 4.825335614909678 & 1.12309E-28 \\ \hline 0.7 & 4.764842187284488 & 4.764842187284488 & 5.96715E-29 \\ \hline 0.8 & 4.696706709347165 & 4.696706709347165 & 1.66422E-28 \\ \hline 0.9 & 4.621609968270664 & 4.621609968270664 & 4.44932E-28 \\ \hline 1.0 & 4.540302305868140 & 4.540302305868140 & 1.75329E-27 \\ \hline \end{tabular}$

Consider 50^th order Gegenbauer Polynomials, i.e. for n=50, we have Eq. (3.106) is

$u(x)=\sum _{k=0}^{50}a_kG_k(x)=a_0G_0(x)+a_1G_1(x)+⋯a_{50}G_{50}(x)$

$u(x)=a_0+2βxa_1+⋯+(-\frac{1}{25}β+⋯x^{50}β^{50})a_{50}$ (3.111)

By Substituting

$u(x)=a_0+2βxa_1+⋯+(-\frac{1}{25}\ β+⋯x^{50}β^{50})a_{50}=5+2x^2-\int _0^x(x-t)[a_0+2βta_1+⋯+(-\frac{1}{25}\ β+⋯t^{50}β^{50})a_{50}]dt.$ (3.112)

Multiply Eq. (3.112) by $G_j\left(x\right),\ j=0,1,...,50$ and integrating both sides from -1 to 1,

$\int _{-1}^1\left[(a_0+2βxa_1+⋯+(-\frac{1}{25}\ β+⋯x^{50}β^{50})a_{50})\right]G_j(x)dx=\int _{-1}^1(5+2x^2)G_j(x)dx+\int _{-1}^1\left[\frac{1}{6}\int _0^x(x-t)\left[(a_0+2βxa_1+⋯+(-1/25β+\dots t^{50}β^{50})a_{50})dt\right]G_j(x)dx,\right]$ (3.113)

Applying the prescribed technique on Eq.(3.113) , we get the following system of equations,

$\left[\begin{matrix}2.3333&1.2309&⋯\ \ \ 0.0384\ \ \\ \ 0&2.9333&⋯\ \ \ \ \ \ 0\\ \ \vdots &\ \ \ \vdots &\vdots \ \ \ \ \ \ \ \ \vdots \\ 0.0589&\ \ 0&⋯\ \ \ \ 5.8950\end{matrix}\right]\left[\begin{matrix}a_0\\ a_1\\ \ \vdots \\ a_{50}\end{matrix}\right]=\left[\begin{matrix}11.333\\ \ \ \ \ 0\\ \ \ \ \ \vdots \\ -0.2746\end{matrix}\right]$

After solving we get,

$a_1=4.88010,\ a_2=5.04811\ and\ \ a_{50}=2.5616\times 10^{-52}.$

Putting the values back we get the approximate solution as,

$u(x)=4.999+9.0109\times 10^{-51}-\dots +2.8840\times 10^{-37}.$

Table 3.11 Comparison of Exact and Approximate Solutions of Eq. (3.104) for n=50 obtained from Gegenbauer polynomials Method

$\begin{tabular}{|c|c|c|c|} \hline X & Exact Solution & Approximate Solution & Error \\ \hline 0.0 & 5.000000000000000 & 5.000000000000000 & 3.86505E-84\\ \hline 0.1 & 4.995004165278026 & 4.995004165278026 &0.00000E+00 \\ \hline 0.2 & 4.980066577841242 & 4.980066577841242 & 0.00000E+00 \\ \hline 0.3 & 4.955336489125606 & 4.955336489125606 & 0.00000E+00 \\ \hline 0.4 & 4.921060994002885 & 4.921060994002885 & 0.00000E+00 \\ \hline 0.5 & 4.877582561890373 & 4.877582561890373 &0.00000E+00 \\ \hline 0.6 & 4.825335614909678 & 4.825335614909678 & 0.00000E+00 \\ \hline 0.7 & 4.764842187284488 & 4.764842187284488 & 0.00000E+00 \\ \hline 0.8 & 4.696706709347165 & 4.696706709347165 & 0.00000E+00 \\ \hline 0.9 & 4.621609968270664 & 4.621609968270664 & 0.00000E+00 \\ \hline 1.0 & 4.540302305868140 & 4.540302305868140 & 0.00000E+00\\ \hline \end{tabular}$

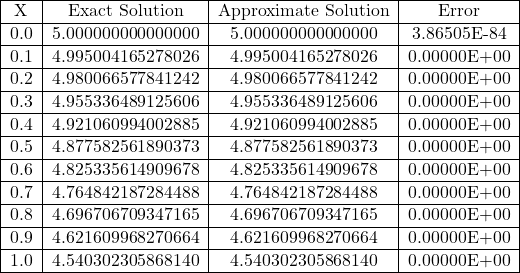
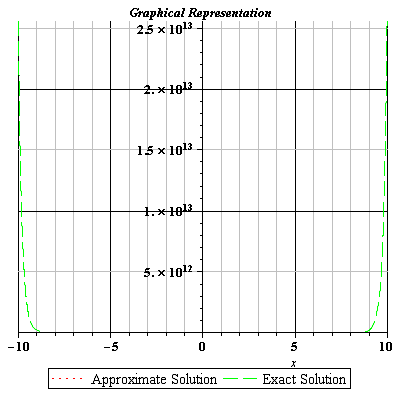
Fig 3.11 Comparison of Exact and Approximate Solutions of Eq. (3.104) for n=50.

3.8.2 Weakly Singular Integral Equation

Consider the Weakly singular Integral equation [2] as

$u(x)=x^2-\frac{128}{45}\ x^{\frac{9}{4}}+\int _0^x\frac{1}{(x-t)^{\frac{3}{4}}}\ u(t)dt.$ (3.115)

The exact solution of Eq. (3.115) is

$u(x)=x^2.$ (3.116)

According to the proposed technique, consider the trail solution

$u(x)=\sum _{k=0}^na_kG_k(x)$ (3.117)

Consider 1^st order Gegenbauer Polynomials, i.e. for n=1, we have Eq. (3.117) is

$u(x)=\sum _{k=0}^1a_kG_k(x)$

$u(x)=a_0G_0(x)+a_1G_1(x).$

$u(x)=a_0+2βxa_1.$ (3.118)

Substituting Eq. (3.118) into Eq. (3.115)

$a_0+2βxa_1=x^2-\frac{128}{45}\ x^{\frac{9}{4}}+\int _0^x\frac{1}{\left((x-t\right)^{\frac{3}{4}}}[a_0+2βta_1]dt.$ (3.119)

Multiply Eq. (3.119) by $G_j\left(x\right),\ j=0,1$ and integrating both sides from 0 to 1, we have

$\int _0^1[a_0+2βxa_1]G_j(x)dx=\int _0^1(x^2-\frac{128}{45}\ x^{\frac{9}{4}})G_j(x)dx+\int _0^1[\int _0^x\frac{1}{(x-t)^{\frac{3}{4}}}\ [a_0+2βta_1]dt]\ G_j(x)dx,\ j=0,1.$ (3.120)

The matrix form of Eq. (3.120) is

$\left[\begin{matrix}-\frac{11}{5}&-\frac{83}{45}\\ -\frac{23}{9}&-\frac{508}{195}\end{matrix}\right]\left[\begin{matrix}a_0\\ a_1\end{matrix}\right]=\left[\begin{matrix}-\frac{317}{585}\\ -\frac{1283}{1530}\end{matrix}\right]$

After solving we get

$a_0=-\frac{1570969}{11841622\ }\ and\ \ a_1=\frac{411751}{455447}.$

Consequently we get approximate solution

$u(x)=-\frac{1570969}{11841622}+\frac{411751}{910894}x.$

Table 3.12 Comparison of Exact and Approximate Solutions of Eq. (3.115) for n=1 obtained from Gegenbauer polynomials Method (GPM)

$\begin{tabular}{|c|c|c|c|} \hline X & Exact Solution & Approximate Solution & Error \\ \hline 0.0 & 0.000000000000000 & -0.132665018400000 & 1.32665E-01\\ \hline 0.1 &0.010000000000000 & -0.042259109480000 &5.22591E-02 \\ \hline 0.2 & 0.040000000000000 & 0.048146799400000 & 8.14680E-3 \\ \hline 0.3 & 0.090000000000000& 0.138552708400000 & 4.85527E-2 \\ \hline 0.4 & 0.160000000000000 & 0.228958617300000 & 6.89586E-02\\ \hline 0.5 & 0.250000000000000 & 0.319364526200000 &6.93645E-02 \\ \hline 0.6 & 0.360000000000000 & 0.409770435100000 & 4.97704E-02 \\ \hline 0.7 & 0.490000000000000 & 0.500176344000000 & 1.01763E-02 \\ \hline 0.8 & 0.640000000000000 & 0.590582253000000 & 4.94177E-02 \\ \hline 0.9 & 0.810000000000000 & 0.680988161900000 & 1.29012E-01 \\ \hline 1.0 & 1.000000000000000 & 0.771394070800000 & 2.28606E-01\\ \hline \end{tabular}$

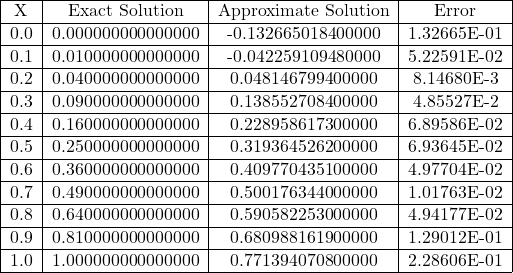
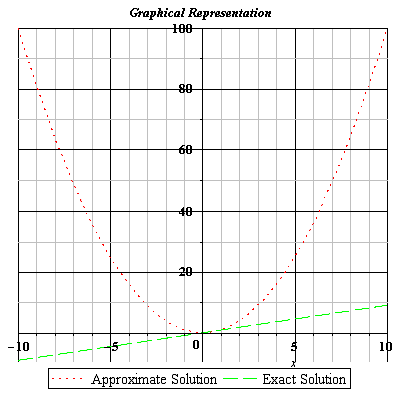
Fig 3.12 Comparison of Exact and Approximate Solutions of Eq. (3.115) for n=1.

Consider 2^nd order Gegenbauer Polynomials, i.e. for n=2, we have Eq. (3.117) is

$\begin{array}{l}u(x)=\sum _{k=0}^2a_kG_k(x)=a_0G_0(x)+a_1G_1(x)+a_2G_2(x).\\ u(x)=a_0+2βxa_1+(2x^2β+2x^2β^2-β)a_2.\end{array}$ (3.121)

Substituting Eq. (3.121) into Eq. (3.115)

$u(x)=a_0+2βxa_1+(2x^2β+2x^2β^2-β)a_2=x^2-128/45x^{\frac{9}{4}}+\int _0^x\frac{1}{(x-t)^{\frac{3}{4}}}[a_0+2βta_1+(2t^2β+2t^2β^2-β)a_2]dt.$ (3.122)

Now multiply Eq. (3.122) by $G_j\left(x\right),\ j=0,1,2$ and integrating both sides from 0 to 1, we have

$\int _0^1[a_0+2βxa_1+(2x^2β+2x^2β^2-β)a_2]G_j(x)dx=\int _0^1(x^2-128/45x^{\frac{9}{4}})G_j(x)dx+\int _0^1[\int _0^x[a_0+2βta_1+(2t^2β+2t^2β^2-β)a_2]dt]G_j(x)dx,\ j=0,1,2.$ (3.123)

The matrix form of Eq. (3.123) is

$\left[\begin{matrix}-\frac{11}{5}&-\frac{83}{45}&\frac{19}{585}\\ -\frac{23}{15}&-\frac{508}{195}&-\frac{611}{765}\\ -\frac{271}{195}&-\frac{1667}{765}&-\frac{23483}{12285}\end{matrix}\right]\left[\begin{matrix}a_0\\ a_1\\ a_2\end{matrix}\right]=\left[\begin{matrix}-\frac{317}{585}\\ -\frac{1283}{1530}\\ -\frac{10139}{12285}\end{matrix}\right]$

After solving we get

$a_0=\frac{1}{4},\ a_1=0\ \ and\ \ a_2=\frac{1}{4}.$

Consequently we have the exact solution is

$u(x)=x^2.$ (3.124)

Table 3.13 Comparison of Exact and Approximate Solutions of Eq. (3.115) for n=2 obtained from Gegenbauer polynomials Method (GPM)

$\begin{tabular}{|c|c|c|c|} \hline X & Exact Solution & Approximate Solution & Error \\ \hline 0.0 & 0.000000000000000 & 0.000000000000000 & 0.00000e+00\\ \hline 0.1 &0.010000000000000 & 0.010000000000000 &0.00000e+00 \\ \hline 0.2 & 0.040000000000000 & 0.040000000000000 & 0.00000e+00 \\ \hline 0.3 & 0.090000000000000& 0.090000000000000 &0.00000e+00 \\ \hline 0.4 & 0.160000000000000 & 0.160000000000000 & 0.00000e+00\\ \hline 0.5 & 0.250000000000000 & 0.250000000000000 &0.00000e+00 \\ \hline 0.6 & 0.360000000000000 & 0.360000000000000 & 0.00000e+00 \\ \hline 0.7 & 0.490000000000000 & 0.490000000000000 & 0.00000e+00 \\ \hline 0.8 & 0.640000000000000 & 0.640000000000000 & 0.00000e+00 \\ \hline 0.9 & 0.810000000000000 & 0.810000000000000 & 0.00000e+00 \\ \hline 1.0 & 1.000000000000000 &1.000000000000000 & 0.00000e+00\\ \hline \end{tabular}$

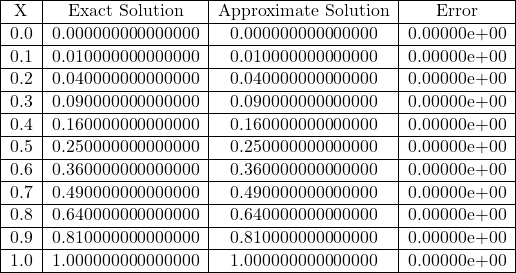
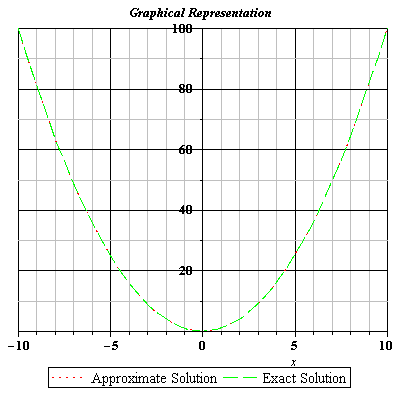
Fig 3.13 Comparison of Exact and Approximate Solutions of Eq. (3.115) for n=2.

3.8.3 Fredholm Integral Equation

Example 3.23 Consider the Fredholm Integral equation [2] as

$u(x)=x^2-x^3+\int _0^1(1-xt)\ u(t)\ dt.$ (3.125)

The exact solution of Eq. (3.125) is

$u(x)=-\frac{29}{90}-\frac{1}{6}x+x^2-x^3.$ (3.126)

According to the proposed technique, consider the trail solution

$u(x)=\sum _{k=0}^na_kG_k(x)$ (3.127)

Consider 2^nd order Gegenbauer Polynomials, i.e. for n=2, we have Eq. (3.127) is

$\begin{array}{l}u(x)=\sum _{k=0}^2α_kG_k(x)=a_0G_0(x)+a_1G_1(x)+a_2G_2(x).\\ u(x)=a_0+2βxa_1+(2x^2β+2x^2β^2-β)a_2\end{array}$ . (3.128)

Substituting Eq. (3.128) into Eq. (3.125)

$u(x)=a_0+2βxa_1+(2x^2β+2x^2β^2-β)a_2=x^2-x^3+\int _0^1(1-xt)[a_0+2βta_1+(2t^2β+2t^2β^2-β)a_2]dt.$ (3.129)

Now multiply Eq. (3.119) by $G_j\left(x\right),\ j=0,1,2$ and integrating both sides from 0 to 1, we have

$\int _0^1[a_0+2βxa_1+(2x^2β+2x^2β^2-β)a_2]G_j(x)dx=\int _0^1(x^2-x^3)G_j(x)dx+\int _0^1[\int _0^1(1-xt)(a_0+2βxa_1+(2x^2β+2x^2β^2-β)a_2))]G_j(x)dx,j=0,1,2.$ (3.130)

Now for $\beta =1$ , the matrix form of Eq. (3.130) is

$\left[\begin{matrix}-\frac{1}{4}&-\frac{1}{3}&-\frac{1}{4}\\ -\frac{1}{3}&-\frac{1}{9}&-\frac{1}{3}\\ -\frac{1}{4}&-\frac{1}{3}&-\frac{211}{180}\end{matrix}\right]\left[\begin{matrix}a_0\\ a_1\\ a_2\end{matrix}\right]=\left[\begin{matrix}\frac{1}{12}\\ \frac{1}{10}\\ \frac{1}{20}\end{matrix}\right]$

After solving we get

$a_0=-\frac{179}{360},\ a_1=\frac{13}{60},\ a_2=-\frac{1}{8}.$

Consequently we have the approximate solution is

$u(x)=-\frac{67}{180}+\frac{13}{180}x-\frac{1}{2}x^2.$

Table 3.14 Comparison of Exact and Approximate Solutions of Eq. (3.125) for n=2 obtained from Gegenbauer polynomials Method (GPM)

$\begin{tabular}{|c|c|c|c|} \hline X & Exact Solution & Approximate Solution & Error \\ \hline 0.0 & -0.322222222200000 & -0.372222222200000 & 5.00000E-02\\ \hline 0.1 &-0.329888888900000 & -0.333888888900000 &4.00000E-03 \\ \hline 0.2 & -0.323555555500000& -0.305555555500000 & 1.80000E-02 \\ \hline 0.3 &-0.309222222200000 & -0.309222222200000 &2.20000E-02 \\ \hline 0.4 & -0.292888888900000 & -0.278888888900000 & 1.40000E-02\\ \hline 0.5 & -0.280555555500000 & -0.280555555500000 &0.00000e+00 \\ \hline 0.6 &-0.278222222200000 & -0.292222222200000 & 1.40000E-02 \\ \hline 0.7 &-0.291888888900000 & -0.313888888900000 & 2.20000E-02 \\ \hline 0.8 &-0.327555555500000 & -0.345555555500000 & 1.80000E-02 \\ \hline 0.9 & -0.391222222200000 & -0.387222222200000 & 4.00000E-03\\ \hline 1.0 & -0.488888888900000 & -0.438888888900000 &5.00000E-02\\ \hline \end{tabular}$

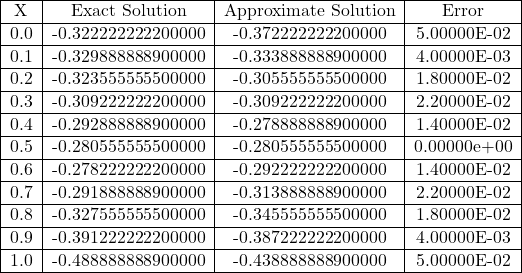
Fig 3.14 Comparison of Exact and Approximate Solutions of Eq. (3.125) for n=2.

Consider 3^rd order Gegenbauer Polynomials, i.e. for n=3, we have Eq. (3.127) is

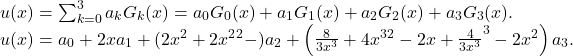$\begin{array}{l}u(x)=\sum _{k=0}^3a_kG_k(x)=a_0G_0(x)+a_1G_1(x)+a_2G_2(x)+a_3G_3(x).\\ u(x)=a_0+2βxa_1+(2x^2β+2x^2β^2-β)a_2+\left(\frac{8}{3x^3}β+4x^3β^2-2βx+\frac{4}{3x^3}β^3-2xβ^2\right)a_3.\end{array}$ (3.131)

Substituting Eq. (3.131) into Eq. (3.125)

$u(x)=a_0+2βxa_1+(2x^2β+2x^2β^2-β)a_2+\left(\frac{8}{3x^3}β+4x^3β^2-2βx+4/3x^3β^3-2xβ^2\right)a_3=x^2-x^3+\int _0^1(1-xt)[a_0+2βta_1+(2t^2β+2t^2β^2-β)a_2+\left(\frac{8}{3t^3}β+4t^3β^2-2βt+\frac{4}{3t^3}β^3-2tβ^2\right)a_3]dt.$ (3.132)

Now multiply Eq. (3.132) by $G_j\left(x\right),\ j=0,1,2,3$ and integrating both sides from 0 to 1, we have

$\int _0^1[a_0+2βxa_1+(2x^2β+2x^2β^2-β)a_2+\left(\frac{8}{3x^3}β+4x^3β^2-2βx+\frac{4}{3x^3}β^3-2xβ^2)a_3]G_j(x)dx=\int _0^1(x^2-x^3)G_j(x)dx+\int _0^1[\int _0^1(1-xt)[a_0+2βta_1+(2t^2β+2t^2β^2-β)a_2+\left(\frac{8}{3t^3}β+4t^3β^2-2βt+\frac{4}{3t^3}β^3-2tβ^2\right)a_3]G_j(x)dx,\right)$ (3.133)

Now for $\beta =1$ equation (3.133) can be written in the matrix form as,

$\left[\begin{matrix}-0.2500&-0.3333&-0.2500\ \ \ -0.1333\\ -0.3333&-0.1111&0.3333\ \ \ \ \ \ \ \ 0.3556\\ -0.2500&0.3333&1.1722\ \ \ \ \ \ \ \ 1.2000\\ =0.1333&0.3556&1.2000\ \ \ \ \ \ \ \ 1.6051\end{matrix}\right]\left[\begin{matrix}a_0\\ a_1\\ a_2\\ a_3\end{matrix}\right]=\left[\begin{matrix}\ \ 0.0833\\ \ \ 0.1000\\ \ \ 0.0500\\ -0.0095\end{matrix}\right]$

After solving we get

$a_0=-\frac{13}{180},\ a_1=-\frac{1}{3},\ a_2=\frac{1}{4}\ and\ a_3=-\frac{1}{8}.$

Consequently we have exact solution as

$u(x)=-\frac{29}{90}-\frac{1}{6}x+x^2-x^3.$

Table 3.15 Comparison of Exact and Approximate Solutions of Eq. (3.125) for n=3 obtained from Gegenbauer polynomials Method

$\begin{tabular}{|c|c|c|c|} \hline X & Exact Solution & Approximate Solution & Error \\ \hline 0.0 & -0.322222222200000 & -0.322222222200000 & 0.00000E+00\\ \hline 0.1 &-0.329888888900000 &-0.329888888900000 &0.00000E+00\\ \hline 0.2 &-0.323555555500000 &-0.323555555500000 & 0.00000E+00\\ \hline 0.3 &-0.309222222200000 & -0.309222222200000 &0.00000E+00 \\ \hline 0.4 & -0.292888888900000 & -0.292888888900000 & 0.00000E+00\\ \hline 0.5 & -0.280555555500000 & -0.280555555500000 &0.00000e+00 \\ \hline 0.6 &-0.278222222200000 & -0.278222222200000 & 0.00000E+00 \\ \hline 0.7 &-0.291888888900000 & -0.291888888900000 & 0.00000E+00 \\ \hline 0.8 &-0.327555555500000 & -0.327555555500000 & 0.00000E+00 \\ \hline 0.9 & -0.391222222200000 & -0.391222222200000 & 0.00000E+00\\ \hline 1.0 & -0.488888888900000 & -0.488888888900000 &0.00000E+00\\ \hline \end{tabular}$

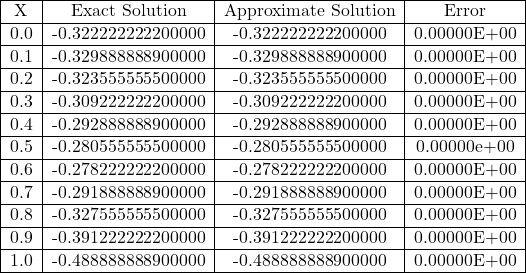
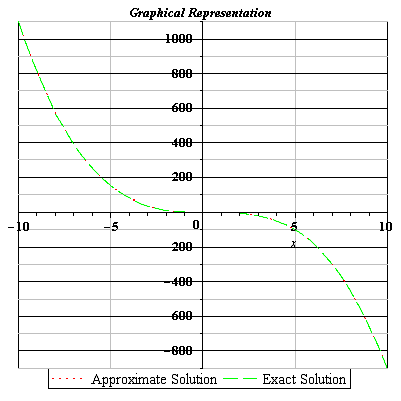
Fig 3.15 Comparison of Exact and Approximate Solutions of Eq. (3.125) for n=3.

References

[1]. H.Exton, New generating function for Gegenbauer polynomial. Computation Applied Mathematics, 67 (1), 191-193, 1996.

[2]. A.M. Wazwaz, Linear and Nonlinear Integral Equations Method and Applications. Springer Heidelberg Dordrecht London, New York. 2011.

[3]. A.M. Wazwaz, Burgers Hierarchy in (2+1)-dimensions: Multiple Kink Solutions and Multiple Singular Kink Solution. International Journal of Nonlinear Science. 10. No.1, 3-11. (2010).