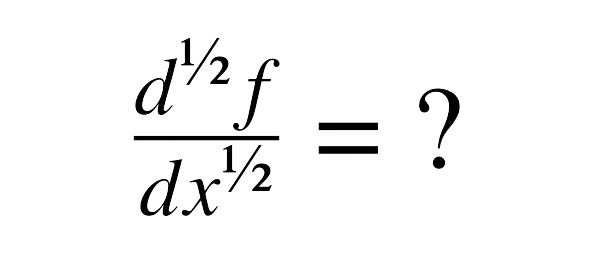
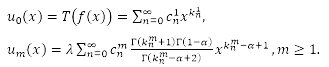ADM and MADM Using Fractional Calculus will be find in this article using different techniques. Many physical phenomena when mathematical modeled yield an integral equation. Many algorithms have been developed to find the exact and approximate solution of linear and nonlinear integral equations. Fettis use the Gauss–Jacobi quadrature rule [4] to determine the a numerical form of the solution of Abel equation, Huang et al. [7] used the Taylor expansion of the unknown function and obtained an approximate solution, latter on Piessens and Verbaeten [11] and Piessens [10] used Chebyshev polynomials to develop an approximate solution to Abel equation, Yousefi used Legender wavelets [14] to present a numerical method for the solution of Abel integral equation. When input signal is with noisy error, Murio et al. [9] suggested a stable numerical solution. Furthermore, Garza et al. [5] and Hall et al. [6] used the wavelet method to invert the inversion of noisy Abel equation, Sunil Kumar et al. [3] used modified Homotopy perturbation to solve the generalized Abel’s equation, Avazzadeh et al. [2] used Chebyshev polynomials to solve Abel’s Integral equations, Wazwaz [12] used efficient method to solve nonlinear integral equations and Abbasbandy [1], and Bhattacharya [3] implemented Bernstein Polynomials in numerical solutions of Volterra integral equations and Hwang and Shih [8] find the solution of integral equations via Laguerre polynomials.
An exact solution of linear and nonlinear equation ,which fully satisfies the equation and approximate solution is close to actual solution.
3.1 Adomian Decomposition Method Using Fractional Calculus
we develop a new algorithm which is mainly based upon Riemann-Liouville fractional derivatives and fractional integral to obtain solutions of linear and nonlinear generalized weakly singular equations. It is observed that the proposed scheme is extremely simple, highly effective, utmost accurate and can be extended to other singular problems.

3.1.1 Methodology
Consider the Weakly Singular equations, we have
![]()
Eq. (3.1) can be converted into initial value problem
 According to the Adomian decomposition method
According to the Adomian decomposition method
 The recurrence relation read as
The recurrence relation read as
 Using the Riemann-Liouville fractional and derivative and fractional integral
Using the Riemann-Liouville fractional and derivative and fractional integral
 We have the recurrence relation
We have the recurrence relation
3.1.2 Weakly Singular Integral Equation
Example 3.1 Consider the following weakly singular integral equation [13] as
![]() Eq. (3.2) can be converted into initial value problem
Eq. (3.2) can be converted into initial value problem
 According to Adomian Decomposition method the recurrence relation read as
According to Adomian Decomposition method the recurrence relation read as
 According to proposed algorithm, we have following approximations
According to proposed algorithm, we have following approximations

u(x) = x
Example 3.2 Consider the following weakly singular integral equation [13] as
![]()
Eq. (3.3) can be converted into initial value problem

According to Adomian Decomposition method the recurrence relation
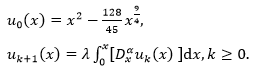
According to proposed algorithm, we have following approximations

Example 3.3 Consider the following weakly singular integral equation [13] as
![]() Eq. (3.4) can be converted into initial value problem
Eq. (3.4) can be converted into initial value problem
 According Adomian Decomposition method the recurrence relation read as
According Adomian Decomposition method the recurrence relation read as
![]() According to proposed algorithm, we have following approximations
According to proposed algorithm, we have following approximations
![]()
According to proposed algorithm, we have following approximations

Example 3.4 Consider the following weakly singular integral equation [13] as
 Eq. (3.5) can be converted into initial value problem
Eq. (3.5) can be converted into initial value problem
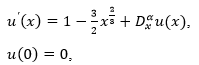 According to Adomian Decomposition method the recurrence relation read as
According to Adomian Decomposition method the recurrence relation read as
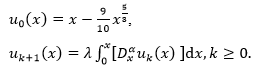 According to proposed algorithm, we have following approximations
According to proposed algorithm, we have following approximations

u(x) = x
Example 3.5 Consider the following weakly singular integral equation [13] as
![]() According to Adomian Decomposition method the recurrence relation read as
According to Adomian Decomposition method the recurrence relation read as
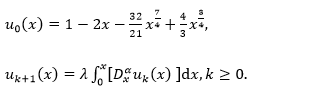 Now according to the proposed algorithm,
Now according to the proposed algorithm,

We have following approximations

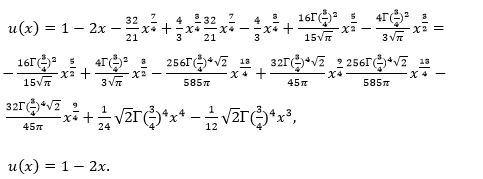
Example 3.6 Consider the following weakly singular integral equation [13] as
![]() According to Adomian Decomposition method the recurrence relation read as
According to Adomian Decomposition method the recurrence relation read as
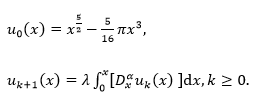 Now according to the proposed algorithm,
Now according to the proposed algorithm,
 We have following approximations
We have following approximations

3.2 Modified Adomian Decomposition Method, using Fractional Calculus.
We develops new algorithm Modified Adomian decomposition method using, fractional calculus which is mainly based upon Riemann-Liouville fractional derivatives and fractional integral to obtain solutions of linear and nonlinear weakly singular equations. It is observed that the proposed scheme is highly effective, utmost accurate and can be extended to other singular problems.
3.2.1 Methodology
Consider the Weakly Singular equations, we have
![]()
Eq. (3.7) can be converted into initial value problem
 According to the Adomian decomposition method
According to the Adomian decomposition method
 The recurrence relation read as
The recurrence relation read as

Using the Riemann-Liouville fractional and derivative and fractional integral
 and
and
![]()
We have the recurrence relation

3.2.2 Weakly Singular Integral Equation
Example 3.8 Consider the following weakly singular integral equation [13] as
![]() Which is equivalent to initial value problem as
Which is equivalent to initial value problem as
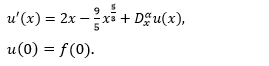 According to Adomian Decomposition method the recurrence relation read as
According to Adomian Decomposition method the recurrence relation read as
 Now according to the proposed algorithm,
Now according to the proposed algorithm,
 We have following approximations
We have following approximations
 Therefore we have
Therefore we have
![]()
Example 3.9 Consider the following weakly singular integral equation [13] as
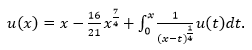 Which is equivalent to initial value problem as
Which is equivalent to initial value problem as
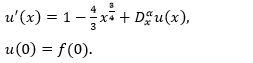 According to Adomian Decomposition method the recurrence relation
According to Adomian Decomposition method the recurrence relation
 Now according to the proposed algorithm,
Now according to the proposed algorithm,
 We have following approximations
We have following approximations
 Therefore we have
Therefore we have
u (x) = x
Example 3.10 Consider the following weakly singular integral equation [13] as
![]() Which is equivalent to initial value problem as
Which is equivalent to initial value problem as
 According to Adomian Decomposition method the recurrence relation read as
According to Adomian Decomposition method the recurrence relation read as
 Now according to the proposed algorithm,
Now according to the proposed algorithm,
 We have following approximations
We have following approximations

Therefore we have
u (x) = x
Example 3.11 Consider the following weakly singular integral equation [13] as
 Which is equivalent to initial value problem as
Which is equivalent to initial value problem as
 According to Adomian decomposition method the recurrence relation read as
According to Adomian decomposition method the recurrence relation read as
 Now according to the proposed algorithm,
Now according to the proposed algorithm,
 We have following approximations
We have following approximations
 Therefore we have
Therefore we have
u (x) = x
Example 3.12 Consider the following weakly singular integral equation [13] as
![]() Which is equivalent to initial value problem as
Which is equivalent to initial value problem as

According to Adomian Decomposition method the recurrence relation read as
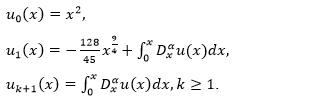 Now according to the proposed algorithm,
Now according to the proposed algorithm,
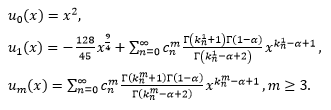
We have following approximations
 Therefore we have
Therefore we have
![]()
Example 3.13 Consider the following weakly singular integral equation [13] as
 Which is equivalent to initial value problem as
Which is equivalent to initial value problem as
 According to Adomian Decomposition method the recurrence relation read as
According to Adomian Decomposition method the recurrence relation read as
![]()
 Now according to the proposed algorithm,
Now according to the proposed algorithm,
 We have following approximations
We have following approximations
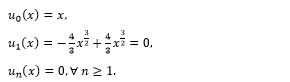 Therefore we have
Therefore we have
u (x) = x
Example 3.14 Consider the following weakly singular integral equation [13] as
![]() which is equivalent to initial value problem as
which is equivalent to initial value problem as
 According to Adomian Decomposition method the recurrence relation read as
According to Adomian Decomposition method the recurrence relation read as
 Now according to the proposed algorithm,
Now according to the proposed algorithm,
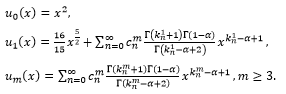 We have following approximations
We have following approximations
![]()
 Therefore we have
Therefore we have
![]()
References
[1]. S. Abbasbandy, Numerical solutions of the integral equations: Homotopy perturbation method and Adomian’s decomposition method, Appl. Math. Comput. 173(23) (2006), 493-500.
[2]. Z. Avazzadeh, B. Shafiee and G. B. Loghmani, Fractional calculus for solving Abel’s integral equations using Chebyshev polynomials, Applied Mathematical Sciences, 5(45)(2011), 2207 – 2216
[3]. Subhra Bhattacharya, Use of bernstein polynomials in numerical solutions of volterra integral equations: Applied Mathematical Sciences, 2(36)(2008), 1773 – 1787.
[4]. M.E. Fettis, On numerical Solution of Equations of the Abel type, Math. Comp. 18(1964), 491–496.
[5]. J. Garza, P. Hall, F.H. Ruymagaart, A new method of solving noisy Abel-type equations, J. Math. Anal. Appl. 257 (2001), 403–419.
[6]. P. Hall, R. Paige, F.H. Ruymagaart, Using wavelet methods to solve noisy Abel-type equations with discontinuous inputs, J. Multivariate. Anal. 86 (2003), 72–96.
[7]. Li Huang, Yong Huang, Xian-Fang Li, Approximate Solution of Abel Integral Equation, Computers and Mathematics with Applications 56 (2008), 1748–1757.
[8]. A. Hwang and Y. P. Shih, Solution of integral equations via Laguerre polynomials, Comput. Electr. Engrg. 9 (1982), 123–129
[9]. D. A. Murio, D.G. Hinestroza, C.W. Mejia, New stable numerical inversion of Abel’s integral equation, Comput. Math. Appl. 11(1992), 3–11.
[10]. R. Piessens, Computing integral transforms and solving integral equations using Chebyshev polynomial approximations, J. Comput. Appl. Math. 121 (2000),113–124.
[11]. R.Piessens, P. Verbaeten, Numerical solution of the Abel integral equation, BIT 13 (1973), 451–457.
[12]. A.M. Wazwaz, A comparison study between the modified decomposition and the traditional Methods for solving nonlinear integral equations, Appl Math. Comput. 181 (2) (2006), 1703 – 1713.
[13]. A.M.Wazwaz, Linear and Nonlinear Integral Equations Method and Applications, Springer Heidelberg Dordrecht London, New York, 2011.