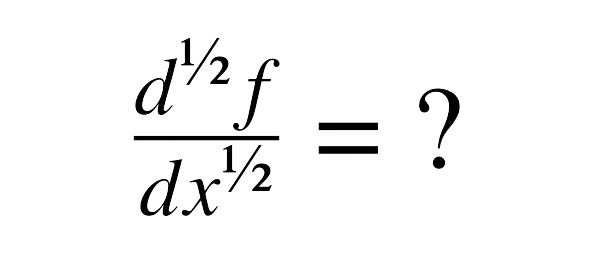
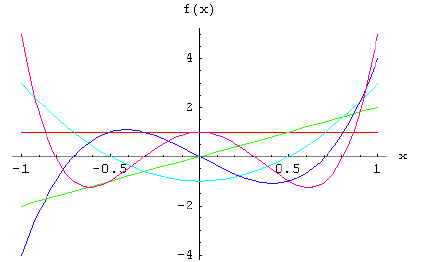
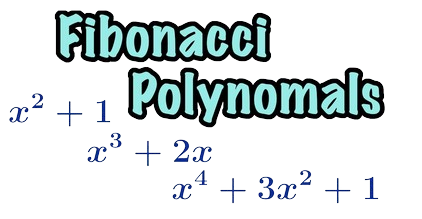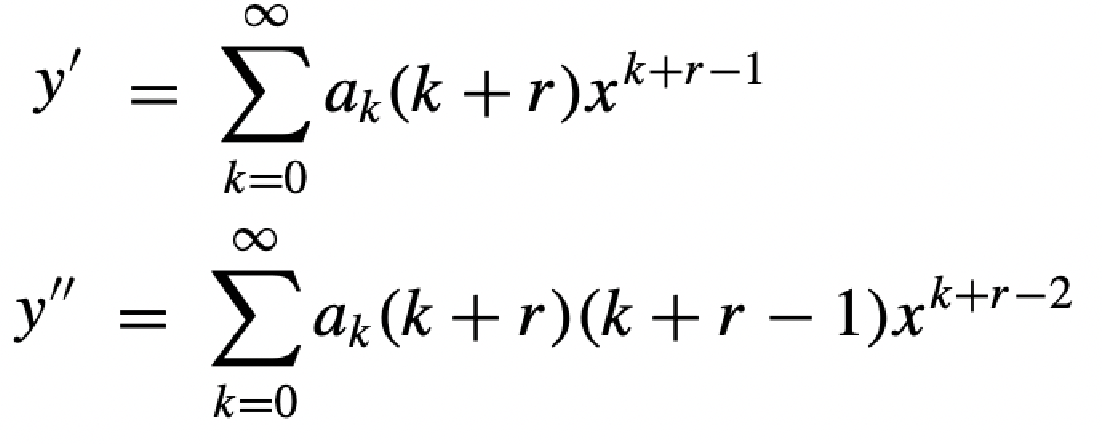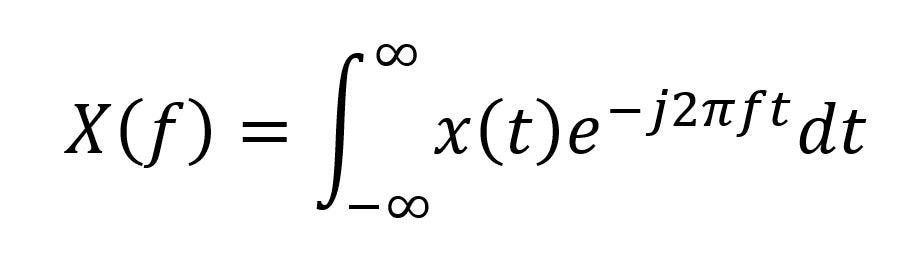Understanding Algebra and use of an Algebra Calculator, it’s a word that evokes both awe and dread. To some, it’s the beautiful backbone of mathematics, while to others, it can feel like a confusing maze […]
The Convolution Theorem Formula
The Convolution Theorem Formula, the Convolution Theorem is an important part of mathematics which connects theory with practice in regards to signal processing or data analysis. Although convoluted in wording, it is definitely one of […]
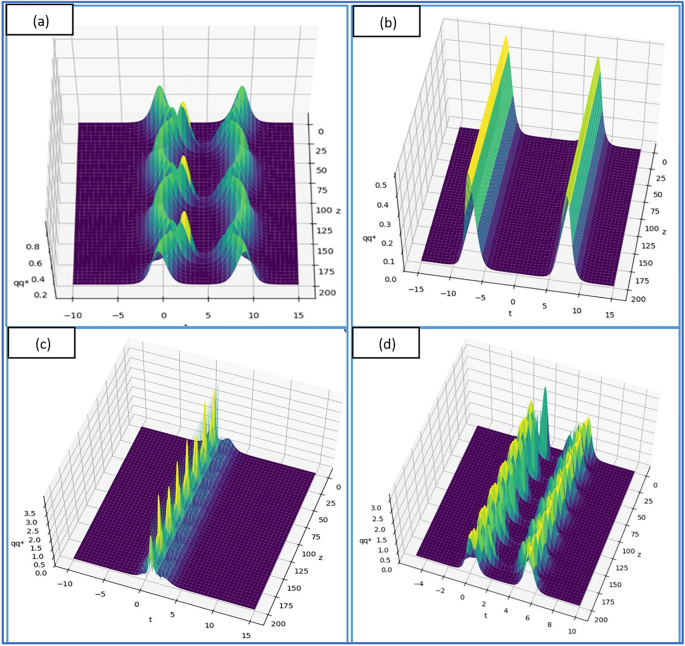
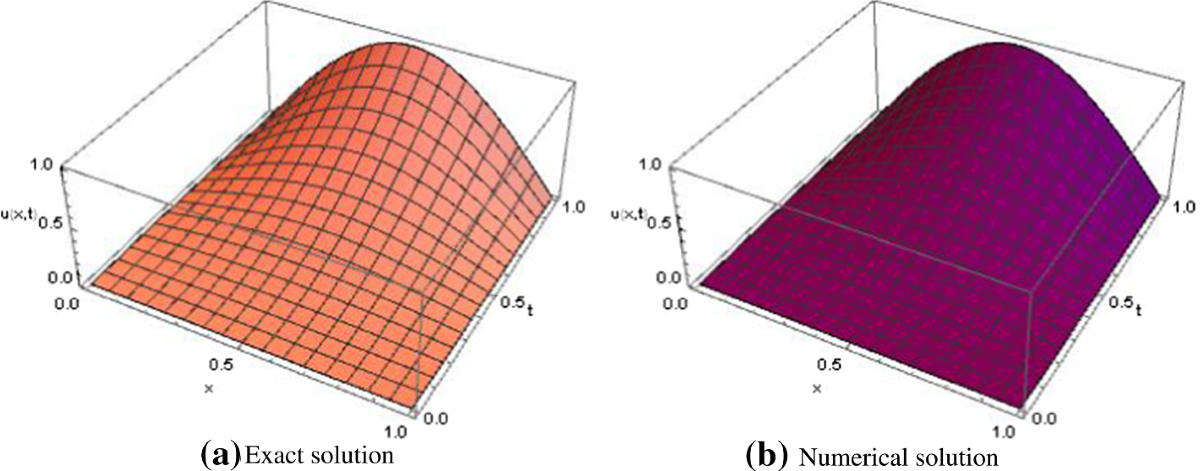
Introduction of Novel Operational Matrices
Introduction of Novel Operational Matrices, may be modified to examine the solution to more diverse problems of a physical nature in intricate geometries. Research was conducted to verify the consistency and aid the mathematical structure […]
Frobenius Method
Frobenius Method, we consider the general second order linear differential equation, (9.1) and attempt to solve it about a regular singular point . For that, we employ the Frobenius method as illustrated in […]
The Fourier Transform
The Fourier Transform ,we move on in our program of decomposing arbitrary functions into sinusoids. We have seen how a periodic function can be expressed as a Fourier series, so now we seek a similar […]
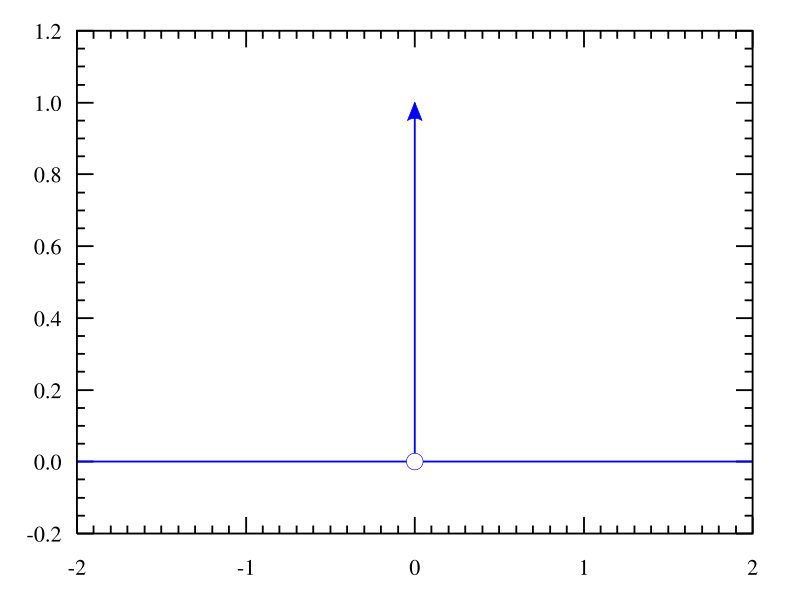
Continuity
Continuity, most of the functions we study in elementary calculus are described by simple formulas. These functions almost always possess derivatives and, in fact, a portion of any first course in calculus is devoted to […]
Initial Value Problems are solved using the Laplace Transform Method
Initial Value Problems are solved using the Laplace Transform Method, as mentioned earlier, the Laplace transform method is very convenient way of solving ordinary differential equations in general and those with constant coefficients in particular. […]
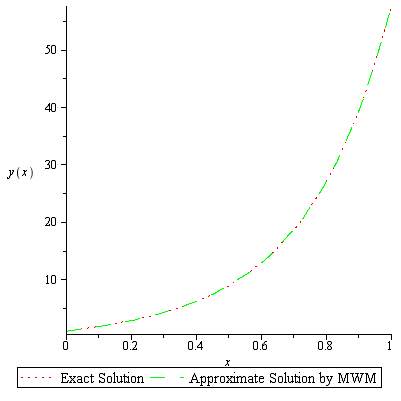
Meixner Wavelet Method
Meixner Wavelet Method,we proposed a new algorithm by inserting Meixner polynomials in traditional Legendre wavelets method. This technique is successively applied to find the exact solution singular ordinary differential equations. The proposed technique is very […]
The Convolution Theorem
The Convolution Theorem, we know that the Laplace transform of a sum of two functions is the sum of the transforms of those functions, i.e., On the same analogy we may think of a similar […]
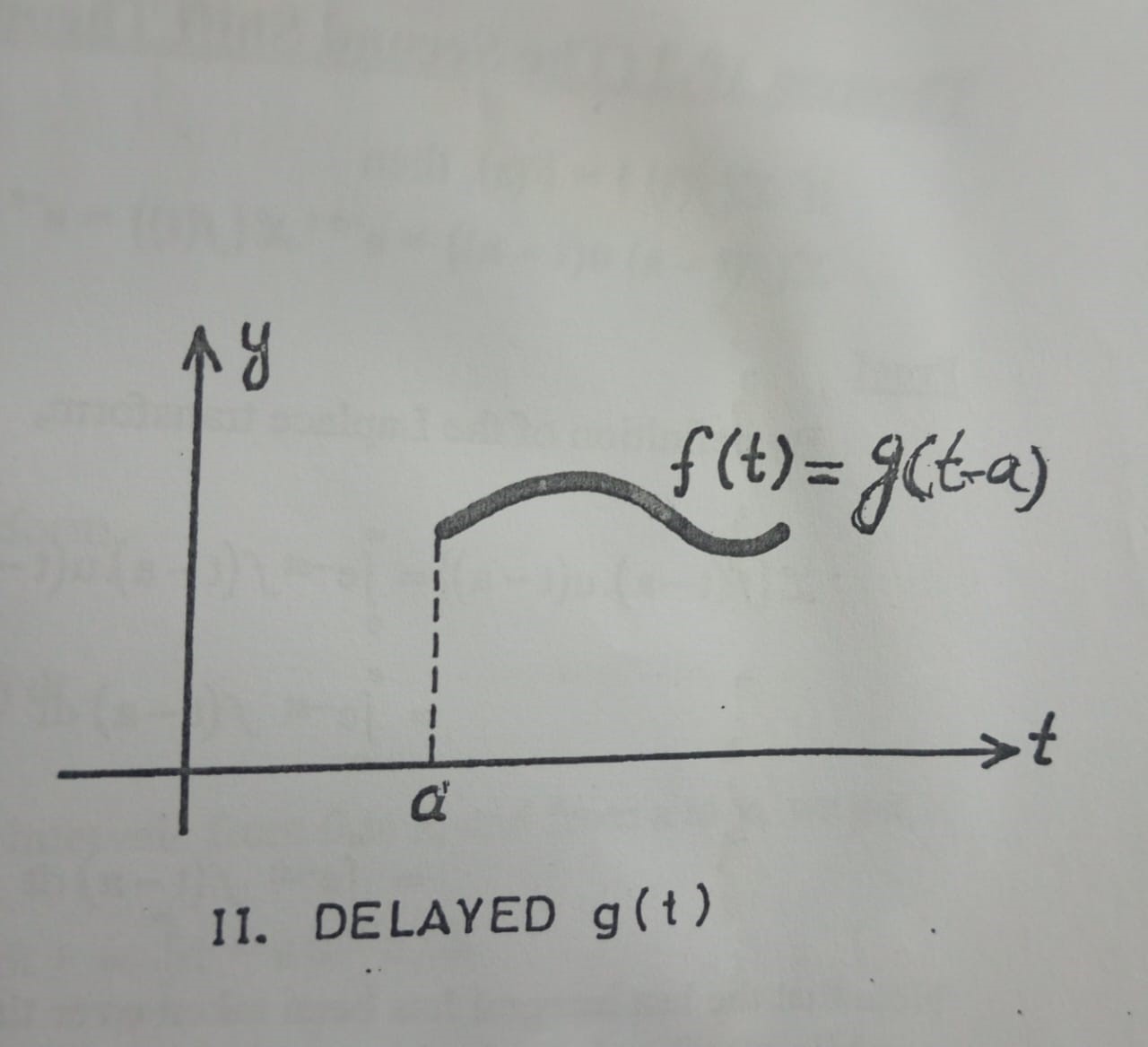
Dirac Delta Function
Dirac Delta Function , the unit step function (or the Heaviside function) helps us in solving differential equations with discontinuous forcing functions. However, there are many problems in Electrical/Mechanical/Mechatronics/Civil Engineering and Physics which involve impulsive […]